Abstract
Composable security definitions, at times called simulation-based definitions, provide strong security guarantees that hold in any context. However, they are also met with some skepticism due to many impossibility results; goals such as commitments and zero-knowledge that are achievable in a stand-alone sense were shown to be unachievable composably (without a setup) since provably no efficient simulator exists. In particular, in the context of adaptive security, the so-called “simulator commitment problem” arises: once a party gets corrupted, an efficient simulator is unable to be consistent with its pre-corruption outputs. A natural question is whether such impossibility results are unavoidable or only artifacts of frameworks being too restrictive.
In this work, we propose a novel type of composable security statement that evades the commitment problem. Our new type is able to express the composable guarantees of schemes that previously did not have a clear composable understanding. To this end, we leverage the concept of system specifications in the Constructive Cryptography framework, capturing the conjunction of several interval-wise guarantees, each specifying the guarantees between two events. We develop the required theory and present the corresponding new composition theorem.
We present three applications of our theory. First, we show in the context of symmetric encryption with adaptive corruption how our notion naturally captures the expected confidentiality guarantee—the messages remain confidential until either party gets corrupted—and that it can be achieved by any standard semantically secure scheme (negating the need for non-committing encryption). Second, we present a composable formalization of (so far only known to be standalone secure) commitment protocols, which is instantiable without a trusted setup like a CRS. We show it to be sufficient for being used in coin tossing over the telephone, one of the early intuitive applications of commitments. Third, we reexamine a result by Hofheinz, Matt, and Maurer [Asiacrypt’15] implying that IND-ID-CPA security is not the right notion for identity-based encryption, unmasking this claim as an unnecessary framework artifact.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 A Plea for Composable Security
Common security definitions found in the literature are game-based, i.e., they require that an adversary cannot win a game that exports certain oracles to the adversary. The goal of such a security game is to capture the adversary’s potential attacks in a minimal manner. However, the mapping of the game’s interface to potential attacks in the real-world use of the cryptographic protocol is commonly not straight-forward. Thus, it is often a-priori unclear which game-based security notion is required in order for the protocol to be secure in a specific application. Rather, that aspect is often informally considered and passed down outside the security definitions, becoming “folklore” over the years.
Composable frameworks, such as [4, 11, 16, 21], on the other hand, provide operational security definitions instead. The way they formalize security is based around comparing the execution of the protocol in the real world to an idealized world that intrinsically has the desired security properties. Importantly, this definition is with respect to any environment, thereby ensuring that the security guarantees not only do not exclude any attacks but also hold irrespective of other protocols (or multiple instances of the same one) being executed. For instance, the composable security definition of a symmetric encryption scheme is the construction of a secure communication channel from an authentic one and a key, with different assumed and constructed channels leading to different notions (e.g., whether replaying is possible). Hence, for a given application it is now trivial to decide whether a certain scheme suffices.
Finally, composable frameworks facilitate modularity. First, they are based on defining components with clean abstraction boundaries (e.g., a secure channel) that abstract away the details of how that module has been constructed (or otherwise obtained). This idealized module can then be used by a higher-level protocol with the security of the combined overall protocol following directly from the composition theorem. Thus, the security of complex protocols can be neatly proven by composing it from smaller sub-protocols.
1.2 Obstacles for Composable Security
While the clear semantics, modularity, and high security guarantees suggest that all protocols should be proven secure in a composable framework rather than in an ad-hoc game-based manner, composable definitions are still not prevalent with the majority of new research still carried out using game-based definitions.
One of the main reasons hindering adoption might be that many primitives are known to be impossible to achieve in the plain UC model, such as zero knowledge [4] and commitments [5]. Furthermore, Lindell has shown [12] that impossibility results are not specific to the UC model but inherent to any kind of similar model based around the existence of an efficient simulator. As a consequence, respective protocols have to rely on additional setup assumptions, such as a common reference string, and are also generally less efficient.
One particular obstacle composable definitions often face is the so-called “simulator commitment problem”, which mainly arises when considering adaptive security. In a nutshell, it describes the simulator’s inability to explain some of its previous choices the moment a party gets corrupted. More concretely, consider the example of two parties securing their communication using symmetric encryption. The intuition is that the adversary does not learn the messages until either of the parties gets corrupted, thereby revealing the key. Before, the adversary should learn at most the length. As a result, the simulator, in the first phase, has to output a fake ciphertexts independent of the real messages. For any semantically secure encryption scheme he can actually do so. This, however, commits him on those fake ciphertexts. At the moment a party gets corrupted, the simulator then needs to be able to explain those ciphertexts by outputting a matching encryption key. Even if he learns all the previous messages, he will not be able to do so for regular encryption schemes. Note, however, that the commitment problem is not restricted to adaptive corruptions only. Similar issues also arise, for instance, in the context of password-based security [7] or identity-based encryption [8], where it has been shown that due to this commitment problem the standard game-based notions do not induce the expected corresponding composable statements.
On a general level, this raises the fundamental question whether such impossibility results actually indicate a security issue, and hence protocols not satisfying the stronger composable definitions should not be used, or whether they present an artifact of the framework. Especially for the commitment problem, the common understanding is that the latter is true. Furthermore, the obstacles are often dealt with by either reverting to composable security with static corruptions only, or by simply retracting to game-based definitions. As a result, there is a clear need for a better composable security notion that lets us settle this question and remedy the issue of the spurious impossibilities.
1.3 Existing Attempts to Overcome the Obstacles
A number of approaches have been proposed in order to circumvent the aforementioned issues of composable security.
First, Canetti and Krawczyk proposed the notion of non-information oracles [6] within the UC-framework. A non-information oracle is essentially a game-based definition embedded into an ideal functionality. For instance, rather than saying that an encryption scheme should realize a secure channel that only leaks the length, the respective functionality leaks the output of the non-information oracle, which is required to satisfy a CPA-like definition. While this circumvents the commitment problem, there are two drawbacks. First, it weakens composition by requiring explicit reductions to the embedded games in the security proof of the higher-level protocols using the functionality. Second, for each ideal functionality a different type of non-information oracle needs to be defined, without providing any generic template. As a consequence, the question of the “right” non-information oracle re-arises, just like when defining a security game.
Second, a line of work considers super-polynomial simulators [3, 20, 22]. The initial proposal by Pass [20] considered sub-exponential simulators and polynomially bounded environments. This implies, however, that the simulator cannot be absorbed into the environment, ceding some of the most fundamental composition properties of the UC-framework. The later works by Prabhakaran and Sahai [22] and Broadnax et al. [3] empower the simulator in a more controlled manner, preserving most natural composition properties. Their adoption, however, still suffers from being rather technical, and moreover, still quite limited in the number of issues they can overcome. For instance, when considering a PRG whose seed might leak, even an all powerful simulator will not be able to explain a truly randomly chosen output with an appropriate seed.
Finally, Backes, Dürmuth, Hofheinz, and Küsters [1] proposed an approach where the real-world resource would just disallow certain activation sequences by the environment that were otherwise impossible to simulate. While this avoids the complications of the other approaches, it scarifies the evident semantics of composable security notions by excluding certain—deemed artificial—attacks. A similar approach has recently been used by Jost, Maurer and Mularczyk in [10].
1.4 Contributions
Interval-wise guarantees. In this work, we propose an alternative solution to the simulator-commitment problem that is aimed at expressing the guarantees of regular schemes within a composable framework. More concretely, we introduce a novel type of construction notion within the Constructive Cryptography (CC) framework that avoids the commitment problem while providing a number of distinct benefits. First, it provides a clean semantics of how the guarantees should be interpreted. Second, it holds in any environment, just as any statement in the CC framework. Third, it is equipped with a composition theorem.
Since the commitment problem usually occurs at a very specific point of the protocol execution, such as when a party gets corrupted, where the security guarantees of the protocol anyway inherently change, our novel construction notion is centered around the very natural idea of formalizing guarantees that hold in a certain interval (between two events). That is, our notion for instance allows to formalize separate security guarantees before and after the corruption event. In contrast to existing simulation-based notions, we thereby only require the simulation to work within each interval, not forcing the simulation to be consistent between the intervals (which causes the initial commitment issues). We discuss how the security guarantees provided by our notion should be interpreted, when stronger notions might still be desirable, and how our notion fits into the space of static versus adaptive security.
Theory extensions. On a technical level, we leverage the specification-based approach of the CC framework, where proving a protocol \(\varvec{\pi }\) to be secure corresponds to modeling the assumed real-world specification \(\mathcal {R}\), and showing that the resulting specification \(\varvec{\pi } \mathcal {R}\) is contained in an ideal specification \(\mathcal {S}\), i.e, \(\varvec{\pi }\mathcal {R} \subseteq \mathcal {S}\).
We formalize interval-wise guarantees as a novel type of specifications within the CC framework. We carefully consider the subtleties arising when defining such specifications and show how they interact with the other aspects of the framework. Finally, we present the respective composition theorem, that actually supersedes all the existing ones, and in particular allows to syntactically combine multiple such interval-wise construction statements, or an interval-wise one with a regular construction statement.
Applications. As a third contribution, we apply our methodology to several examples. First, we consider the encrypt-then-MAC paradigm in a setting where the keys can adaptively leak to the adversary, stylizing adaptive passive corruptions. Using our interval-wise guarantees, we obtain a simple composable security definition thereof without the need for non-committing encryption. More concretely, we consider the following three properties. First, we require the messages to be confidential as long as neither the encryption nor the authentication key leaked. (An IND-CPA secure scheme cannot guarantee confidentiality without authenticity.) In our definition, this is phrased as the construction of a secure channel up to that point. Second, between the exposure of the encryption key and the authentication key, we require communication to still be authentic, i.e., an authenticated channel to be constructed. Finally, after the encryption key has been exposed, we still require correctness.
As a second application, we show a composable formalization of information-theoretically binding commitment schemes realizable in the plain model. We then show how, based on such a commitment scheme, Blum’s protocol constructs a composable coin-toss notion. Applying composition then directly implies that this formalization can be achieved in the plain model as well. While the resulting specification is obviously too weak to serve as a common reference string, it guarantees unbiasedness. Hence, it is provides a good enough type of randomness resource whenever unbiasedness is sufficient, in particular formalizing and formally validating the intuitive-level argumentation about flipping a coin over the telephone of the corresponding papers of that time.
Finally, we consider the composable guarantees of identity-based encryption. We revisit the result by Hofheinz, Matt, and Maurer [8] that shows the standard \(\mathsf {ind\text {-}id\text {-}cpa}\) notion to be too weak when considering a traditional composable statement based on the existence of a single simulator, even when considering static corruptions, due to the commitment problem. Furthermore, the authors have shown that the same weaker construction that actually can be achieved, could also be achieved by a weaker game-based notion \(\mathsf {ind\text {-}id1\text {-}cpa}\), modeling so-called lunch-time attacks. We refute their results in the following way: Based on interval-wise guarantees we formalize a composable specification of IBE that corresponds exactly to the standard \(\mathsf {ind\text {-}id\text {-}cpa}\) notion.
1.5 Outline
In Sect. 3, we provide a introduction to our notion, before presenting the technical details in Sect. 4. In Sect. 5 we present a novel composable definition of perfectly binding commitments and its application to coin tossing. In the full version [9], we moreover revisit composable security of identity-based encryption.
2 Preliminaries: Constructive Cryptography
This work builds upon some more recent aspect of the Constructive Cryptography (CC) framework [13, 16]. We therefore revisit the key aspects thereof, follows the exposition introduced in [16], with some adaptations from [10].
2.1 Resources, Converters, and the Interaction Model
At its heart, the Constructive Cryptography framework views cryptography as a resource theory, in which parties use certain resources (e.g., communication channels and a shared secret key) to construct another resource via a protocol.
Global events. In this work, we use the version of Constructive Cryptography introduced in [10] that enriches the interaction model by a notion of globally observable events. Formally, events are a generalization of monotone binary outputs (MBO) introduced by Maurer et al. [15]. Roughly, an MBO is a value that can change from 0 to 1 but not back, which can be interpreted as a single event happening once the MBO changes to 1. An event then just corresponds to a named MBO and the global event history \(\mathcal {E}\) is a list of event names without duplicates (to model that every event can occur at most once). For an event name \(n\), we denote by \(\mathcal {E}\overset{+}{\leftarrow }\mathcal {E}^{\mathsf {}}_{n}\) the act of appending \(n\) to \(\mathcal {E}\) (or leaving it unchanged if it is already contained). Moreover, we use \(\mathcal {E}^{\mathsf {}}_{n}\) as a short-hand notation to denote that \(n\) is in the list \(\mathcal {E}\), and say that the event happened. Finally, we denote by \(\mathcal {E}^{\mathsf {}}_{n_1} \prec \mathcal {E}^{\mathsf {}}_{n_2}\) that the event \(n_1\) precedes the event \(n_2\) in the event history.
Resources. A resourceFootnote 1 \(\mathsf {R}\) is a reactive system that interacts in the following two ways with the rest of the world: First, it allows interaction at one or several named communication interfaces, in the following just called interfaces, at which it can be queried an input x, and must answer with an output y at the same interface. Second, during an activation, the resource \(\mathsf {R}\) can depend on the global event history \(\mathcal {E}\), and can furthermore append events from a predefined set of names. We call this set of names the events controlled by \(\mathsf {R}\).
Formally, resources are modeled as random systems [14], where the interface address, the actual input x, and the current state of the event history are encoded as part of the input. Analogously, the answer y and the new state of the event history are encoded as part of the output, under the constraint that the old state of the event history is a prefix of the new one. For the sake of this paper, a reader unfamiliar with the CC framework might however just think of a resource as the behavior of an oracle machine, where each interface corresponds to an oracle and the event history being similar to the “directory” ITI used in the recent version of UC [4]. Note, however, that a resource only defines the behavior of the system and not its description, i.e., two different (pseudo-code descriptions of) ITMs having the same input-output behavior denote the same resource.
A set of resources can be viewed as a single one, with the interface set of the composed resource being the union. For resources \(\mathsf {R}_1, \ldots , \mathsf {R}_n\) (with disjoint interface sets) we denote by \([\mathsf {R}_1, \ldots , \mathsf {R}_n]\) the parallel composition.
Converters and protocols. In the Constructive Cryptography framework, converters express the local action executed by one party. A converter expects to be connected to a given number of interfaces at the “inside”, and emulates a certain set of interfaces at the “outside”. Upon an input at an outside interface, the converter is allowed to make a bounded number of oracle queries to the inside interfaces, before returning a value at the queried interface.
For a converter \(\pi \) and a resource \(\mathsf {R}\), let \(\mathcal {I}\) denote a tuple describing an injective mapping from \(\pi \)’s inside interfaces to interfaces of \(\mathsf {R}\). We then denote by  the resource obtained from connecting the converter accordingly. The resource \(\mathsf {R}'\) no longer exposes those interfaces but the ones emulated by \(\pi \) instead. Converter attachment satisfies the natural property of composition order independence, stating that the composition order does not matter—only the final system does.
the resource obtained from connecting the converter accordingly. The resource \(\mathsf {R}'\) no longer exposes those interfaces but the ones emulated by \(\pi \) instead. Converter attachment satisfies the natural property of composition order independence, stating that the composition order does not matter—only the final system does.
Proposition 1
Let \(\pi _1\) and \(\pi _2\) be two converters, let \(\mathsf {R}\) be a resource and let \(\mathcal {I}_1\) and \(\mathcal {I}_2\) be such that they assign disjoint interfaces. Then, \(\pi _1^{\mathcal {I}_1} \pi _2^{\mathcal {I}_2} \mathsf {R} = \pi _2^{\mathcal {I}_2} \pi _1^{\mathcal {I}_1} \mathsf {R}\). Moreover, if \(\mathsf {S}\) is another resource such that the interface sets of \(\mathsf {R}\) and \(\mathsf {S}\) are disjoint, then we have \(\pi _1^{\mathcal {I}_1} \bigl [\mathsf {R}, \mathsf {S}\bigr ] = \bigl [\pi _1^{\mathcal {I}_1} \mathsf {R}, \mathsf {S}\bigr ]\).
We define a protocol to be a set of converter-connection pairs, i.e,.  with pairwise disjoint \(\mathcal {I}_i\)’s. Moreover, we say that \(\varvec{\pi }\) is a protocol for a resource \(\mathsf {R}\), if \(\mathsf {R}\) has all the required interfaces for the protocol application to be well-defined, and write \(\varvec{\pi } \mathsf {R}\) to denote its application.
with pairwise disjoint \(\mathcal {I}_i\)’s. Moreover, we say that \(\varvec{\pi }\) is a protocol for a resource \(\mathsf {R}\), if \(\mathsf {R}\) has all the required interfaces for the protocol application to be well-defined, and write \(\varvec{\pi } \mathsf {R}\) to denote its application.
The environment (distinguisher). The distinguisher \(\mathsf {D}\) is a special type of environment that first interacts with a resource \(\mathsf {R}\) by making queries to the resource’s interfaces. Between two such queries it can access the global event history and append events to it, except the ones controlled by \(\mathsf {R}\). Note that activations are atomic, i.e., at any moment in time either the resource or the distinguisher is activated, but not both. Finally, the distinguisher ends the interaction with the resource by outputting a bit. The advantage of \(\mathsf {D}\) is then defined as

where we use the syntax \(\mathsf {D}^{\mathcal {E}}(\cdot )\) to make explicit that the distinguisher has oracle access to the global event history \(\mathcal {E}\).
2.2 Constructions
Specifications. It is natural to consider only certain desired (or assumed) properties of a system and deliberately not specify others. Some of those choices are intrinsic to the mathematical model we use, such as only considering the input-output behavior and ignoring the physical aspects. Other properties can be purposefully ignored by considering specifications of systems that simply leave out those aspects, focusing only on the relevant properties. Following [17], we model specifications as sets of resources \(\mathcal {R}\) that all have the same interface set. For each property, such as confidentiality, one has in mind, one can consider the set \(\mathcal {R}\) of resources satisfying that property. Vice versa, each set of resources \(\mathcal {R}\) can be interpreted as the set of properties common to all elements. For instance, authenticated communication might be modeled as the set of all communication channels that are authentic—not specifying the level of confidentiality by including both confidential as well as non-confidential channels.
Constructions as subsets. In provable security one typically considers the execution of a protocol \(\varvec{\pi }\) that makes use of some assumed specification \(\mathcal {R}\), such as a communication network or a public-key infrastructure. In short, one wants to show that the specification  satisfies the desired security properties. As explained in the previous section, those properties are formalized as a specification \(\mathcal {S}\), and thus proving security means proving \(\varvec{\pi } \mathcal {R} \subseteq \mathcal {S}\). Note that obviously the guarantees given by \(\mathcal {S}\) are generally weaker than the ones by \(\varvec{\pi } \mathcal {R}\). The purpose of such a statement is, however, that the security properties are in \(\mathcal {S}\) both more explicit and simpler to analyze. In other words, the goal is to distill out the relevant properties and abstract away the others.
satisfies the desired security properties. As explained in the previous section, those properties are formalized as a specification \(\mathcal {S}\), and thus proving security means proving \(\varvec{\pi } \mathcal {R} \subseteq \mathcal {S}\). Note that obviously the guarantees given by \(\mathcal {S}\) are generally weaker than the ones by \(\varvec{\pi } \mathcal {R}\). The purpose of such a statement is, however, that the security properties are in \(\mathcal {S}\) both more explicit and simpler to analyze. In other words, the goal is to distill out the relevant properties and abstract away the others.
Traditionally, the statement \(\varvec{\pi } \mathcal {R} \subseteq \mathcal {S}\) is read as the protocol \(\varvec{\pi }\) constructing the specification \(\mathcal {S}\) from the specification \(\mathcal {R}\), or in UC-jargon the protocol securely realizing the specification \(\mathcal {S}\) in the \(\mathcal {R}\)-hybrid model. Hence, as a shorthand notation we introduce the following construction notion.
Definition 1
Let \(\mathcal {R}\) and \(\mathcal {S}\) be specifications, and let \(\varvec{\pi }\) be a protocol for \(\mathcal {R}\). Then, we say that \(\varvec{\pi }\) constructs \(\mathcal {S}\) from \(\mathcal {R}\), denoted  , if and only if \(\varvec{\pi } \mathcal {R} \subseteq \mathcal {S}\), i.e.,
, if and only if \(\varvec{\pi } \mathcal {R} \subseteq \mathcal {S}\), i.e.,

In slight abuse of notation, we write  in lieu of
in lieu of  for singleton specifications.
for singleton specifications.
This construction notion is associated with the usual composition properties of Constructive Cryptography: sequential and parallel composition—which form the equivalence of the universal composition theorem of the UC-framework.
Theorem 1
Let \(\mathcal {R}\), \(\mathcal {S}\), and \(\mathcal {T}\) be arbitrary specifications, and let \(\varvec{\pi }\) and \(\varvec{\pi }'\) be arbitrary protocols for \(\mathcal {R}\) and \(\mathcal {S}\), respectively. Then, we have
-
1.
 ,
, -
2.
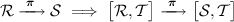 .
.
Proof
The first property follows directly from the transitivity of the subset relation, \(\varvec{\pi }' \bigl (\varvec{\pi } \mathcal {R}\bigr ) \subseteq \varvec{\pi }' \mathcal {S} \subseteq \mathcal {T}\), and the second property follows from Proposition 1: \(\varvec{\pi } \bigl [\mathcal {R},\mathcal {T}\bigr ] = \bigl [\varvec{\pi } \mathcal {R},\mathcal {T}\bigr ] \subseteq \bigl [\mathcal {S}, \mathcal {T}\bigr ]\).
The specifications \(\varvec{\pi } \mathcal {R}\) and \(\mathcal {S}\) are often referred to as real- and ideal-world, respectively, according to the so-called real-world/ideal-world paradigm on which most composable frameworks [4, 11, 16, 21] are based. Following that paradigm, security statement affirm that the real word is “just-as-good” as the ideal world, meaning that for all parties, no matter whether honest or adversarial, it does not make a difference whether they live in the real (where an arbitrary element of \(\varvec{\pi } \mathcal {R}\) is present), or in the ideal world (where some element of \(\mathcal {S}\) is present). Hence, if the honest parties are content with the guarantees they get from the ideal specification, they can safely execute the protocol in the real world instead.
The (in)existence of a simulator. Simulation-based security turned out to be one of the most fundamental concepts in cryptography and is closely linked with the real-world/ideal-world paradigm. It not only forms the foundation of semantic security, zero knowledge, and the security of MPC, but also of virtually every composable framework. Whereas the former definitions tend to require an after-the-fact simulation of the transcript, composable frameworks get their stronger guarantees from requiring on-line simulation, where an adaptive environment interacts with the simulator. The common understanding of those security definitions is then that the simulator “translates” the attacks from the real-world adversary to the ideal world such that they achieve the same effect.
While the initial version of the Constructive Cryptography framework also hard-coded the existence of a simulator (with respect to the dummy adversary), starting from [17], the simulator is no longer an integral part of the construction notion. Rather, employing a simulator is just one way of defining an ideal specification, \(\varvec{\sigma }\mathcal {S}\) that makes the achieved security properties obvious. For instance, the specification of confidential channels can then be written as the specification \(\mathcal {S}\) of channels that only leak the message length, combined with an arbitrary simulator. From this description it is apparent that for any resource in the combined specification \(\varvec{\sigma }\mathcal {S}\), only the length is leaked.
If one restricts oneself to specifications of this type, then the following more specific composition theorem can be deduced.
Proposition 2
Let \(\mathcal {R}\), \(\mathcal {S}\), and \(\mathcal {T}\) be specifications, and let \(\varvec{\pi }\) and \(\varvec{\pi }'\) be protocols for \(\mathcal {R}\) and \(\mathcal {S}\), respectively. For any simulators \(\varvec{\sigma }\) (for \(\mathcal {S}\)) and \(\varvec{\sigma }'\) (for \(\mathcal {T}\)), such that the set of interfaces controlled by the simulators are disjoint from the ones controlled by the protocols, we have
-
1.
 ,
, -
2.
 .
.
Proof
By composition order invariance we have \(\varvec{\pi }' \varvec{\sigma }\mathcal {S} = \varvec{\sigma }\varvec{\pi }' \mathcal {S} \subseteq \varvec{\sigma }\varvec{\sigma '} \mathcal {T}\), implying  . The first property then follows directly from combining this with Theorem 1. The second property follows from Theorem 1 and Proposition 1 as well: \(\varvec{\pi }[\mathcal {R}, \mathcal {T}] = [\varvec{\pi }\mathcal {R}, \mathcal {T}] \subseteq [\varvec{\sigma }\mathcal {S}, \mathcal {T}] = \varvec{\sigma }[\mathcal {S}, \mathcal {T}]\). \(\square \)
. The first property then follows directly from combining this with Theorem 1. The second property follows from Theorem 1 and Proposition 1 as well: \(\varvec{\pi }[\mathcal {R}, \mathcal {T}] = [\varvec{\pi }\mathcal {R}, \mathcal {T}] \subseteq [\varvec{\sigma }\mathcal {S}, \mathcal {T}] = \varvec{\sigma }[\mathcal {S}, \mathcal {T}]\). \(\square \)
2.3 Relaxations
The basic construction notion does not take into account statistical errors or computational assumptions. Those aspects are formalized by so-called relaxations, as introduced in [17]. On an abstract level, a relaxation is a mapping from specifications to weaker, so-called relaxed, specifications. For our purpose, where we instantiate specifications by sets of resources, we can define a relaxation as a function mapping a single resource to a set of resources.
Definition 2
Let \(\varTheta \) denote the set of all resources. A relaxation \(\phi \) is a function \(\phi :\varTheta \rightarrow 2^\varTheta \) (where \(2^\varTheta \) denotes the power set of \(\varTheta \)) such that \(\mathsf {R} \in \phi (\mathsf {R})\) for all \(\mathsf {R} \in \varTheta \). In addition, for a specification \(\mathcal {R}\), we define  as a shorthand notation.
as a shorthand notation.
A concrete relaxation thereby formalizes some notion of resources being “almost-as-good” in some context. That is, if we were happy with constructing a resource specification \(\mathcal {S}\), then we should also be happy with \(\mathcal {S}^\phi \), if we believe the weakening \(\phi \) to be justifiable in the given context. For instance, one could consider the relaxation that maps the resource \(\mathsf {R}\) to the set of all computationally indistinguishable resources from \(\mathsf {R}\) under some computational assumption. Hence, if we believe the computational assumption to be valid, we should be as content with the relaxed specification as with the original one.
Abstracting away irrelevant properties is a core paradigm of any modular analysis. Applied to Constructive Cryptography, this means that ideally we should be able to “forget” relaxations. That is, if one shows that one protocol constructs \(\mathcal {S}^\phi \) (from some assumed resources), one should be able to compose it with another statement that assumes \(\mathcal {S}\) instead. On the most abstract level, it is easy to see that the following rules apply to any relaxation.
Proposition 3
For any specifications \(\mathcal {R}\) and \(\mathcal {S}\), and any relaxation \(\phi \), we have
-
1.
\(\mathcal {R} \subseteq \mathcal {R}^\phi \),
-
2.
\(\mathcal {R} \subseteq \mathcal {S} \Longrightarrow \mathcal {R}^\phi \subseteq \mathcal {S}^\phi \),
-
3.
\((\mathcal {R} \cap \mathcal {S})^{\phi } \subseteq \mathcal {R}^{\phi } \cap \mathcal {S}^{\phi }\),
-
4.
\((\mathcal {R} \cup \mathcal {S})^{\phi } = \mathcal {R}^{\phi } \cup \mathcal {S}^{\phi }\).
Proof
All properties trivially follow from \(\mathsf {R} \in \phi (\mathsf {R})\).
The reduction relaxation. We now introduce the most fundamental relaxation, which captures computational security based on explicit reductions. This is defined as a function \(\epsilon \) that maps distinguishers to their respective performance in [0, 1], where \(\epsilon (\mathsf {D})\) typically refers to the winning probability of a modified distinguisher \(\mathsf {D}'\) (the reduction) on the underlying computational problem.
Definition 3
Let \(\epsilon \) be a function that maps distinguishers to a value in [0, 1]. Then, the induced relaxation on a resource \(\mathsf {R}\), denoted \(\mathsf {R}^\epsilon \), is defined as

We call such a relaxation generally an \(\epsilon \)-relaxation or reduction relaxation.
We now discuss several properties that \(\epsilon \)-relaxations have. First, the errors just add up, as expressed by the following theorem.
Theorem 2
Let \(\mathcal {R}\) be an arbitrary specification, and let \(\epsilon _1\) and \(\epsilon _2\) be arbitrary \(\epsilon \)-relaxations. Then we have \(\bigl (\mathcal {R}^{\epsilon _1}\bigr )^{\epsilon _2} \subseteq \mathcal {R}^{\epsilon _1 + \epsilon _2}\).
Proof
This follows directly from the triangle inequality of the distinguishing advantage.
Second, they naturally commute with protocol application and parallel composition of additional resources, i.e., the relaxation can be “pulled out”. In such a step, however, the additional resource or converter has to be explicitly accounted for in the reduction.
Theorem 3
The \(\epsilon \)-relaxation is compatible with protocol application in the following sense that \(\varvec{\pi }\left( \mathcal {R}^\epsilon \right) \subseteq \left( \varvec{\pi } \mathcal {R} \right) ^{\epsilon _{\varvec{\pi }}}\), for  , where \(\mathsf {D} \varvec{\pi }(\cdot )\) denotes the distinguisher that first attaches \(\varvec{\pi }\) to the given resource and then executes \(\mathsf {D}\). Moreover, it is compatible with parallel composition, i.e., \(\bigl [\mathcal {R}^\epsilon , \mathcal {S}\bigr ] \subseteq [\mathcal {R}, \mathcal {S}]^{\epsilon _{\mathcal {S}}}\), for
, where \(\mathsf {D} \varvec{\pi }(\cdot )\) denotes the distinguisher that first attaches \(\varvec{\pi }\) to the given resource and then executes \(\mathsf {D}\). Moreover, it is compatible with parallel composition, i.e., \(\bigl [\mathcal {R}^\epsilon , \mathcal {S}\bigr ] \subseteq [\mathcal {R}, \mathcal {S}]^{\epsilon _{\mathcal {S}}}\), for  , where \(\mathsf {D}[\,\cdot \,, \mathsf {S}]\) denotes the distinguisher that emulates \(\mathsf {S}\) in parallel to the given resource and then lets \(\mathsf {D}\) interact with them.
, where \(\mathsf {D}[\,\cdot \,, \mathsf {S}]\) denotes the distinguisher that emulates \(\mathsf {S}\) in parallel to the given resource and then lets \(\mathsf {D}\) interact with them.
Proof
The proof can be found in the full version [9].
The composition theorem with \(\epsilon \)-relaxations then follows directly from these compatibility results. The following corollary phrases the corresponding result—which in older version of Constructive Cryptography used to be called the composition theorem, thereby hard-coding computational security.
Corollary 1
For any specifications \(\mathcal {R}\), \(\mathcal {S}\), and \(\mathcal {T}\), any protocols \(\varvec{\pi }\) and \(\varvec{\pi '}\), and any \(\epsilon \)-relaxation \(\epsilon \) and \(\epsilon '\), we have
-
1.
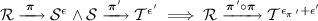 ,
, -
2.
 ,
,
where \(\epsilon _{\varvec{\pi }}\) and \(\epsilon _{\mathcal {S}}\) are defined as in Theorem 3, respectively.
Proof
The proof can be found in the full version [9].
3 Interval-Wise Guarantees: Motivation and Intuition
In this section, we outline the general approach, and its motivation, proposed in this work, before we deep dive into the technicalities in Sect. 4. In particular, we believe that the conceptual contributions are of interest independent from the exact mathematical formalization.
3.1 A Motivating Example
Consider two parties, Alice and Bob, who want to communicate securely over the Internet. If they have a pre-shared secret key available, e.g. from running a key agreement protocol, then it is well known that the encrypt-then-MAC paradigm achieves the desired goal. Assuming independent keys for the encryption and MAC scheme, this construction is secure if the underlying encryption scheme is IND-CPA secure and the MAC scheme is weakly unforgeable.
What, however, if we assume that in reality the keys to not be one hundred percent secure? Intuitively one should expect the scheme to remain secure until either of the keys leak to an adversary, and the security properties then to gracefully downgrade accordingly. More concretely, there is little reason to doubt the following security guarantees should be provided by the scheme:
-
1.
until either of the keys leak, the scheme should provide both confidentiality and authenticity;
-
2.
if only the encryption key leaked so far, then the scheme should still provide authenticity;
-
3.
once the MAC key leaked, the scheme should at least still provide correctness, i.e., allow the parties to communicate in the absence of an active network attack.
(Note that if first the MAC key gets exposed, then a scheme that is only IND-CPA secure might not provide full confidentiality.)
3.2 A Naive Attempt
While the encrypt-then-MAC paradigm has composably proven to be sound in a context where both parties are honest and the keys are secure (e.g. [6, 18]), extending those results to deal with key exposures has turned out to be surprisingly strenuous.
Intuitively, one might model the achieved security guarantees as an secure channel with downgradable security, which waives confidentiality and authenticity once the respective keys leaked. The protocol should then construct such a channel from an insecure channel and two leakable keysFootnote 2, for authentication and encryption, respectively. See Fig. 1 for a formal definition of the respective resources \(\mathsf {InsecCh}\), \(\mathsf {AuthKey}\), and \(\mathsf {EncKey}\) (for the assumed resources), and \(\mathsf {SecCh}\) for the secure channel with downgradable security. Following the paradigm of modularity, one might try to formalize and prove this in two steps and first consider authentication only, as modeled by a downgradable authenticated channel \(\mathsf {AuthCh}\) (c.f. Fig. 1 as well). Indeed, one can show the following construction.
Proposition 4
Let \(\mathsf {AuthCh}\) denote the authenticated channel that degrades its security once the respective key is leaked, as formally defined in Fig. 1, and let \(\varvec{\pi }_{\mathsf {MAC}}\) denote the simple protocol that applies a MAC scheme to the messages. Then, there exists a simulator \(\varvec{\sigma }_{\mathsf {MAC}}\) such that

where \(\epsilon _{\mathsf {MAC}}\) denotes a simple reduction to the MAC-forgery game.
Proof
This is a well-known result, which has for instance been sketched in [13].
However, once we turn our attention towards the second construction step—using encryption to achieve confidentiality—we run into the so-called simulator commitment problem of composable security, as expressed by the following proposition.
Proposition 5
Let \(\mathsf {SecCh}\) denote a secure channel that degrades the respective guarantees once the keys have been exposed, as depicted in Fig. 1, and let \(\varvec{\pi }_{\mathsf {ENC}}\) be the protocol that applies a symmetric encryption scheme. For any (efficient) simulator \(\varvec{\sigma }_{\mathsf {ENC}}\), and (an efficiency preserving) reduction \(\epsilon _{\mathsf {CPA}}\) to the IND-CPA game, we have

i.e., IND-CPA security does not suffice.
Proof (Sketch)
In the first phase, the simulator has to produce, without knowing the message, fake ciphertexts \(c_1, c_2, \ldots , c_n\) that look indistinguishable from the real one. For an IND-CPA secure scheme, he can easily do so by encrypting an arbitrary message of the correct length. The moment the encryption key leaks in the real world, he however has to output a uniformly looking key that makes his ciphertexts decrypt to the correct messages. Even knowing the messages by now, this is infeasible unless we assume a non-committing encryption scheme. Furthermore, as long as the requested key is shorter than n, Nielsen [19] showed that NCE cannot be achieved in the standard model by non-interactive protocols.
Of course one could avoid this impossibility by utilizing stronger primitives and/or assumptions, such as non-committing encryption. In some contexts, such as when considering deniability, their stronger guarantees might even be inherently necessary. In this work, we however pose the following question: How can we express the aforementioned security guarantees, that the encrypt-then-MAC paradigm using regular encryption intuitively does provide, in a composable framework? That is, rather than establishing a stronger security notion, we aim at expressing the exact guarantees provided by existing game-based notions.
3.3 Our Solution
So how to express the natural properties that are achieved? First, let us have another look at the reason for the impossibility: traditional simulation-based security notions require the simulator to commit to a ciphertext, emulating the encryption, based on the length only. Even if the simulator later gets to learn the entire message, it cannot come up with an encryption key that decrypts the previously output ciphertext to this message. Observe, however, that outputting the length only is just a technical way of expressing confidentiality until either one of the keys leak. In principle, there is no inherent requirement for a consistent simulation strategy across the different phases of the experiments. This is exactly what our proposal of interval-wise guarantees builds on: allowing disjoint simulation strategies for different phases of a protocol run. In other words, we simply make three disjoint security statements, one guaranteeing confidentiality and authenticity until either key is leaked, one only guaranteeing authenticity between the exposure of the encryption key and the MAC key, and one guaranteeing correct delivery of messages afterwards. Given the specification centric approach of Constructive Cryptography, this can be phrased as
where \(\mathcal {S}_1\) to \(\mathcal {S}_3\) are specifications formalizing the respective guarantees.
Phrasing separate statements can trivially be done in any framework, but also comes with a number of drawbacks. First, having to specify three constructions of unconnected, potentially differently described, specifications incurs a certain cognitive overhead, making the overall achieved security more demanding to understand. Second, and more severely, one loses some compositional properties. In particular, the analysis of another protocol building on top of those guarantees would require to make the exact same case distinction.
To overcome those drawbacks, we phrase each guarantee as an appropriate interval-wise relaxation of the same underlying resource: the downgradable secure channel. That is, we phrase security as
where \(\phi _1\) to \(\phi _3\) formalize the interval-wise relaxations. Another protocol can then simply assume the overly idealized downgradable secure channel \(\mathsf {SecCh}\), with our novel composition theorem taking care of devising the appropriate overall security statement. We formalize this type of relaxation and the corresponding composition theorem in the next section, i.e., Sect. 4.
Translating the approach to another composable framework, such as UC, might be feasible but non-trivial. First, one might try to formalize a single interval-wise guarantee as a different corruption model, where for instance the adversary simply does not get the encryption key to securely realize a functionality analogon to \(\mathsf {SecCh}\). To then compose this step with a \(\mathsf {SecCh}\)-hybrid statement, one would probably require some compiler translating the statement. We, thus, believe that formalizing our results in CC that allows for arbitrary specifications is both simpler and more natural.
A remark on adaptive versus static security. Our security statement makes a static case separation on the intervals considered. This might raise the question as to how this differs from simply considering static corruptions only. We would like to stress that our statement is about a real-world system, where the environment gets to adaptively (depending on all the outputs it sees) choose when the appropriate keys are leaked. Hence, our notion lies somewhere in between the traditional notions of static and adaptive security.
To which extent our notion suffices in practice, and when a stronger traditional adaptive statement is required, is in our opinion an interesting open research problem. On the one hand, fully adaptively secure notions, without doubt, play a crucial role as a technical tool in many cryptographic constructions. On the other hand, very few cases are known where the overall security of an application actually seems to be meaningfully impacted by adaptiveness. For instance, consider the folklore example of an MPC protocol where an adversary knows which party she has to corrupt based on some observed value during the execution. Nevertheless, for a polynomially sized adversary structure (i.e., choices which parties to corrupt), the adversary could still guess upfront, implying that even traditional static security would suffice. This is for instance the case if there are only logarithmically (or constant) many parties overall.
Moreover, even if there super-polynomially many choices, it could still be that our interpretation of the static result is wrong: if we distinguish n static cases, and in each one of them a certain property is violated with probability \(\epsilon \), then all we can say is that by the union bound the probability of a property being violated is bounded by \(n \epsilon \). Hence, concluding from \(\epsilon \) being negligible that the protocol is overall secure, might simply not be sound in the first place.
A remark on stronger security guarantees. The primary goal of this work is to express the security guarantee of certain schemes in a composable framework, for which so far this has not been possible. This does not contradict stronger security notions, such as non-committing encryption, being of use as well. For instance, insisting that the simulator can explain the ciphertexts (in the traditional notion) formalizes that the ciphertexts are never of any value—in a broader sense than confidentiality. This might play an important role in advanced properties such as deniability, or e.g. in a scenario where an adversary wants to prove to another party that he managed to wiretap the channel before the transmitted message and the corresponding encryption key are publicly announced. Phrasing that no adversary can succeed requires the simulator to work beyond the public announcement, and achieving it requires non-committing encryption. Otherwise, committing to the ciphertext ahead of the public announcement should convince the other party.
4 Interval-Wise Guarantees: Definitions
In this section, we formalize interval-wise guarantees as a type of relaxation and provide the corresponding composition theorem. In the spirit of modularity, we proceed in several steps. First, we introduce one relaxation that waives all guarantees after a certain point, and second, the complementary one that waives all guarantees before a certain event. Third, we combine those relaxations and show that it fits well into the existing theory. Finally, we present the resulting construction notion and phrase the motivating example therein.
4.1 Guarantees up to Some Point
As we have seen in the motivational example, the confidentiality of the messages should be guaranteed until the key is leaked. To phrase this, we, on a high level, only require that the simulator works up to this event. We formalize this as a novel type of relaxation consisting of all systems behaving equally up to this point. To this end, for a resource \(\mathsf {R}\), we consider the modified resource that halts once a certain predicate on the global event history is satisfied.
Definition 4
Let \(\mathsf {R}\) denote a resource, and let \(P(\mathcal {E})\) denote a monotone predicate on the global event history. That is, if \(\mathcal {E}\) is a prefix of \(\mathcal {E}'\) then \(P(\mathcal {E}) \rightarrow P(\mathcal {E}')\). Then, we denote by \({\text {until}}_{P}(\mathsf {R})\) the resource that behaves like \(\mathsf {R}\) but halts the moment \(P(\mathcal {E})\) becomes true. That is, it no longer triggers any further events and all subsequent (including the one for the query that triggered the condition) answers are the special symbol \(\bot \).
Getting back to our example, consider the resource \({\text {until}}_{P}(\mathsf {SecCh})\) for  , depicted in Fig. 2. Since this resource no longer produces any output once either event occurred, it clearly never leaks the messages to Eve and removes Eve’s capability of injecting messages. Hence, the resulting resource closely matches the expected secure channel when ignoring key exposures.
, depicted in Fig. 2. Since this resource no longer produces any output once either event occurred, it clearly never leaks the messages to Eve and removes Eve’s capability of injecting messages. Hence, the resulting resource closely matches the expected secure channel when ignoring key exposures.
The secure channel from Fig. 1 when halted once either key leaks. In contrast to the original one, this resource never leaks the actual messages.
We now define the according relaxation, which maps a system to the set of all systems that behave equivalently up to some event.
Definition 5
Let \(P\) be a monotone predicate on the global event history, indicating until when the behavior must be the same as the one of the resource \(\mathsf {R}\). Then, the induced relaxation on a resource \(\mathsf {R}\), denoted \(\mathsf {R}^{P]}\), is defined as

We call such a relaxation generally an until-relaxation.
As with the \(\epsilon \)-relaxation, the statements only become reusable and thus truly composable if we understand how the until-relaxation interacts with the other elements of the framework. For this, first observe that equality up to some point is monotone, i.e., if two resources are equivalent up to some point, they are also equivalent up to every earlier point. This furthermore implies that two until-relaxations add up in the natural manner, as follows.
Theorem 4
Let \(\mathsf {R}\) and \(\mathsf {S}\) be two resources, and let \(P_1\) and \(P_2\) be two monotone predicates. Then, we have
In particular, for every specification \(\mathcal {R}\), we have \(\mathcal {R}^{P_1]} \subseteq \bigl (\mathcal {R}^{P_1]}\bigr )^{P_2]} \subseteq \mathcal {R}^{P_1 \vee P_2]}\).
Proof
The first property follows directly from the definition of the \({\text {until}}_{}()\) projection. In order to prove the second property, let \(\mathsf {S} \in \bigl (\mathcal {R}^{P_1]}\bigr )^{P_2]}\). Then, there exists \(\mathsf {T} \in \mathcal {R}^{P_1]}\) such that \({\text {until}}_{P_2}(\mathsf {S}) = {\text {until}}_{P_2}(\mathsf {T})\). Moreover, there exists \(\mathsf {R} \in \mathcal {R}\) such that \({\text {until}}_{P_1}(\mathsf {T}) = {\text {until}}_{P1}(\mathsf {R})\). By the first property we, thus, obtain \({\text {until}}_{P_1 \vee P_2}(\mathsf {S}) = {\text {until}}_{P_1 \vee P_2}(\mathsf {T}) = {\text {until}}_{P_1 \vee P_2}(\mathsf {R})\), concluding the proof. \(\square \)
Furthermore, on a positive note, the relaxation is compatible with both protocol application and parallel composition, as expressed by the following theorem. Those compatibility properties—analogously to Corollary 1—also directly imply sequential and parallel composition properties. For the lack of use, we however omit explicitly stating them.
Theorem 5
The until-relaxation is compatible with protocol attachment, i.e., \(\varvec{\pi }\bigl (\mathcal {R}^{P]}\bigr ) \subseteq \bigl (\varvec{\pi }\mathcal {R}\bigr )^{P]}\) and with parallel composition, i.e., \(\bigl [\mathcal {R}^{P]}, \mathcal {S}\bigr ] \subseteq \bigl [\mathcal {R},\mathcal {S}\bigr ]^{P]}\).
Proof
A proof is presented in the full version [9].
Unfortunately, however, the until-relaxation does not commute directly with the \(\epsilon \)-relaxation, as expressed by the following theorem.
Theorem 6
There exist specifications \(\mathcal {R}\) and \(\mathcal {S}\), a monotone predicate \(P\), and a function \(\epsilon \) mapping distinguishers to values in [0, 1] such that
Proof
The proof can be found in the full version [9].
This not only raises the question which order actually corresponds to the intuitive interpretation of such a combination—the set of all systems which behave equally until the condition is triggered assuming the assumption of \(\epsilon \) is valid—but also restricts reuse of such statement. That is, if one construction assumes \(\mathcal {S}^{P]}\) to obtain \(\mathcal {T}\), and another one constructs \(\mathcal {S}^\epsilon \) instead, then adjusting the former construction to assume \(\mathcal {S}^\epsilon \) instead is non-trivial. As a consequence, we will introduce a combined relaxation in Sect. 4.3, resolving both issues.
4.2 Guarantees From Some Point On
In this section, we now consider the complementing type of guarantees: guarantees that only hold from a certain point on. Formalizing such guarantees in a model where an adaptive environment interacts with the resource is, however, quite delicate. In this work, we thus opt for a rather simple (and restricted) version of it, where we use again a monotone condition on the global event history. We then define the projection that disables access to a system \(\mathsf {R}\) before that condition is met. Clearly, the condition must rely on “external” events only (the ones not controlled by \(\mathsf {R}\)), i.e., satisfying it must not require accessing the resource itself.
Definition 6
Let \(P(\mathcal {E})\) denote a monotone predicate on the global event history. For a resource \(\mathsf {R}\), let \({\text {from}}_{P}(\mathsf {R})\) denote the resource that behaves like \(\mathsf {R}\), except that it only accepts queries once \(P(\mathcal {E})\) is true (and before only returns \(\bot \)).
For instance, the resource \({\text {from}}_{\mathcal {E}^{\mathsf {leaked}}_{\mathsf {EncKey}}}(\mathsf {SecCh})\) only answers queries once the environment triggered the event \(\mathcal {E}^{\mathsf {leaked}}_{\mathsf {EncKey}}\). Thus, in contrast to \(\mathsf {SecCh}\), this resource always leaks the full message of the adversary, in line with our intuition that it describes the behavior after the key has been exposed.
Based on this projection, we now introduce the corresponding relaxation.
Definition 7
Let \(P(\mathcal {E})\) be a monotone predicate, indicating from which point on the behavior must be the same as the one of the resource \(\mathsf {R}\). Then, the induced relaxation on a resource \(\mathsf {R}\), denoted \(\mathsf {R}^{[P}\), is defined as

We call such a relaxation generally a from-relaxation.
The way the from-relaxation interacts with the other elements of the theory is analogous to the until-relaxation. First, two from-relaxations add up naturally: if we relax the guarantees offered by a specification to only hold from the moment \(P_1\) is satisfied, and then further relax them to only hold once \(P_2\) is satisfied, then the guarantees only hold once \(P_1 \wedge P_2\) is satisfied.
Theorem 7
Let \(\mathsf {R}\) and \(\mathsf {S}\) be two resources, and let \(P_1\) and \(P_2\) be monotone predicates on the global event history. Then, we have
In particular, for every specification \(\mathcal {R}\), we have \(\mathcal {R}^{[P_1} \subseteq \bigl (\mathcal {R}^{[P_1}\bigr )^{[P_2} \subseteq \mathcal {R}^{[P_1 \wedge P_2}\).
Proof
The proof is analogous to the one of Theorem 4.
Second, the relaxation is compatible with protocol application and parallel composition, which moreover implies that it graciously interacts with the basic construction notion.
Theorem 8
The from-relaxation is compatible with protocol application, i.e., \(\varvec{\pi }\bigl (\mathcal {R}^{[P}\bigr ) \subseteq \bigl (\varvec{\pi }\mathcal {R}\bigr )^{[P}\) and with parallel composition, i.e., \(\bigl [\mathcal {R}^{[P}, \mathcal {S}\bigr ] \subseteq \bigl [\mathcal {R},\mathcal {S}\bigr ]^{[P}\).
Proof
The proof is analogous to the one of Theorem 5.
Analogously to the until-relaxation, the from-relaxation, however, does not commute with the \(\epsilon \)-relaxation.
Theorem 9
There exist specifications \(\mathcal {R}\) and \(\mathcal {S}\), a monotone predicate \(P(\mathcal {E})\), and a function \(\epsilon \) mapping distinguishers to values in [0, 1] such that
Proof
A proof can be found in the full version [9] of this report.
Finally, consider the interaction between the from- and the until-relaxation. While the from-projection and the until-projection commute, i.e.,
it is an interesting open question whether the two respective relaxations actually commute. As a consequence, we introduce a combined from-until relaxation in the next subsection.
4.3 The Interval-Wise Relaxation
As we have seen, the \(\epsilon \)-relaxation commutes neither with the until-relaxation nor the from-relaxation, and its unclear whether the from- and until-relaxations do. This impedes modularity and reusability of the statements and also deteriorates their intuitive semantics: if for instance we want to express that a system behaves like a certain ideal up to some point, and under certain computational assumptions, which order of the relaxations is the right one and should be proven? To alleviate those issues, in this section, we introduce two combined relaxations that build on the atomic ones introduced in the previous section. We then show that they both have natural semantics and clean properties.
First, we consider a relaxation that combines the from- and until-relaxation, thereby alleviating the issue that those relaxations might not commute.
Definition 8
Let \(P_1(\mathcal {E})\) and \(P_2(\mathcal {E})\) be two monotone predicates, indicating from when until when the resource must behave like \(\mathsf {R}\). We then define the following relaxation

While this combined relaxation apparently neither corresponds to \(\bigl (\mathsf {R}^{[P_1}\bigr )^{P_2]}\) nor \(\bigl (\mathsf {R}^{P_2]}\bigr )^{[P_1}\), it interestingly corresponds to the transitive closure thereof. Taking the transitive closure, moreover, also restores symmetry, i.e., \(\mathsf {S} \in \mathsf {R}^{[P_1,P_2]} \Leftrightarrow \mathsf {R} \in \mathsf {S}^{[P_1,P_2]}\), lost by each of the two individual combinations. Overall, this indicates that the combined relaxation best corresponds to the intuition of the “almost-as-good” relation it should intuitively represent.
Theorem 10
For any resource \(\mathsf {R}\) and any monotone predicates \(P_1\) and \(P_2\), we have
where \(\mathsf {R}^{\phi _1 \cdot \phi _2 \cdots \phi _n}\) is a shorthand notation for first applying \(\phi _1\), then \(\phi _2\), until \(\phi _n\).
Proof
The proof can be found in the full version [9].
We can now leverage this alternative definition to directly derive properties about the combined relaxations based on the proven properties of the two underlying ones. In particular, we can show that two such relaxations add up in the expected manner and are compatible with both protocol application as well as parallel composition.
Theorem 11
For every specification \(\mathcal {R}\), and all monotone predicates \(P_1\), \(P_2\), \(P_1'\), and \(P_2'\), we have \(\bigl (\mathcal {R}^{[P_1,P_2]}\bigr )^{[P_1',P_2']} \subseteq \mathcal {R}^{[P_1 \wedge P_1',P_2 \vee P_2']}\).
Proof
This follows directly by combining Theorems 4, 7 and 10.
Theorem 12
The combined relaxation is both compatible with protocol application, i.e., \(\varvec{\pi }\bigl (\mathcal {R}^{[P_1,P_2]}\bigr ) \subseteq \bigl (\varvec{\pi }\mathcal {R}\bigr )^{[P_1,P_2]}\) and with parallel composition, i.e., \(\bigl [\mathcal {R}^{[P_1,P_2]}, \mathcal {S}\bigr ] \subseteq \bigl [\mathcal {R},\mathcal {S}\bigr ]^{[P_1,P_2]}\).
Proof
By Theorem 10 we have that \(\mathcal {R}^{[P_1,P_2]} = \Bigl (\bigl (\mathsf {R}^{[P_1}\bigr )^{P_2]}\Bigr )^{[P_1}\). Using the compatibility of the from-relaxation and until-relaxation, i.e., Theorems 5 and 8, directly implies the desired properties. \(\square \)
As we have seen, neither the until- nor the from-relaxation commute with the computational \(\epsilon \)-relaxation, and the same holds true for the from-until-relaxation as well. As a consequence, neither \((\mathsf {R}^{[P_1,P_2]})^\epsilon \) nor \((\mathsf {R}^\epsilon )^{[P_1,P_2]})\) seems to capture the set of all systems that behave like \(\mathcal {R}\) in the interval \([P_1,P_2]\) assuming that the computational problem encoded in \(\epsilon \) is hard. In the spirit of the combined from-until relaxation, we solve this issue by introducing a combined relation. Since the \(\epsilon \) relaxation is not idempotent, but the epsilons add up, taking the transitive closure, however, does not match the desired relaxation but the following restricted version of transitive closure does.
Definition 9
For two monotone predicates \(P_1\) and \(P_2\), and a function \(\epsilon \) mapping distinguishers to values in [0, 1], we define the following relaxation:

and call such a relaxation an interval-wise relaxation.
We now prove that the interval-wise relaxation has all the desired properties.
Theorem 13
Let \(P_1\) and \(P_2\) be two monotone predicates, and let \(\epsilon \) be a function mapping distinguishers to values in [0, 1]. Then, for any specification \(\mathcal {R}\) we have
where  , i.e., the performance of the distinguisher interacting with the projected resource, and analogously for \(\epsilon '_{[P_1 \wedge P_1',P_2 \vee P_2']}\).
, i.e., the performance of the distinguisher interacting with the projected resource, and analogously for \(\epsilon '_{[P_1 \wedge P_1',P_2 \vee P_2']}\).
Proof
The proof can be found in the full version [9].
Theorem 14
The interval-wise relaxation is compatible with protocol application, i.e., \(\varvec{\pi }\bigl (\mathcal {R}^{[P_1,P_2] : \epsilon }\bigr ) \subseteq \bigl (\varvec{\pi }\mathcal {R}\bigr )^{[P_1,P_2] : \epsilon _{\varvec{\pi }}}\) and with parallel composition, i.e., \(\bigl [\mathcal {R}^{[P_1,P_2] : \epsilon }, \mathcal {S}\bigr ] \subseteq \bigl [\mathcal {R},\mathcal {S}\bigr ]^{[P_1,P_2] : \epsilon _{\mathcal {S}}}\).
Proof
By definition we have  . Using the compatibility of the \(\epsilon \)-relaxation and the from-until-relaxation, i.e., Theorems 3 and 12, directly implies the result.
. Using the compatibility of the \(\epsilon \)-relaxation and the from-until-relaxation, i.e., Theorems 3 and 12, directly implies the result.
4.4 The Resulting Construction Notion
Based on the interval-wise relaxation, we now introduce our new construction notion. To this end, let \(\varOmega \) denote a set of tuples \((P_1, P_2, \epsilon , \varvec{\sigma })\), where \(P_1\) and \(P_2\) are monotone predicates on the global event history, \(\epsilon \) is a function mapping distinguishers to values in [0, 1], and \(\varvec{\sigma }\) denotes a simulator. We then consider constructions of the following type:

That is, each element in \(\varOmega \) describes a time-interval in which the elements in \(\varvec{\pi }\mathcal {R}\) can be abstracted as elements in \(\mathcal {S}\)—with respect to the simulator \(\varvec{\sigma }\) and error \(\epsilon \).
Application to the running example. In our example, we want to phrase that the symmetric encryption protocol constructs the secure channel from the authenticated one and the key in the corresponding intervals.
Proposition 6
Let \(\varvec{\pi }_{\mathsf {ENC}} = (\pi _{\mathsf {enc}}, \pi _{\mathsf {dec}})\) denote the protocol securing communication using a symmetric encryption scheme. Then, for the resources in Fig. 1, there exist (efficient) simulators \(\varvec{\sigma _1}\), \(\varvec{\sigma _2}\), and \(\varvec{\sigma _3}\) such that

for

where \(\epsilon _{\mathsf {CPA}}\) denotes a simple reduction from distinguishing the secure and authenticated channel (without key leakage) to the IND-CPA game.
Proof
A proof sketch is presented in the full version [9] of this report.
Composition. Finally, we finish the section by stating the composition guarantees of this type of construction statement. It follows directly from the properties proven about the interval-wise relaxation in Theorems 13 and 14.
Theorem 15
Let \(\mathcal {R}\), \(\mathcal {S}\), and \(\mathcal {T}\) be arbitrary specifications, let \(\varvec{\pi }\) and \(\varvec{\pi }'\) be arbitrary protocols, and let \(\varOmega \) and \(\varOmega '\) be arbitrary interval-wise guarantees. Then, we have

where  . Furthermore, we have
. Furthermore, we have

Proof
The proof is stated in the full version [9].
Note that this construction notion subsumes all those previously introduced in this work. In particular, instantiating \(P_1 = \mathtt {true}\), \(P_2 = \mathtt {false}\), \(\epsilon (\mathsf {D}) = 0\), and \(\varvec{\sigma }= \mathsf {id}\), i.e., the identity converter, yields \((\mathsf {id} \mathcal {S})^{[\mathtt {true},\mathtt {false}] : 0} = \mathcal {S}\). As a consequence, the above composition theorem also allows to combine constructions according to each of the notions introduced in this work. For instance, in our example, we can compose the construction of \(\mathsf {AuthCh}\) from Proposition 4 (according to the standard notion) with the interval-wise construction of \(\mathsf {SecCh}\) from Proposition 6.
5 Application to Commitments and Coin-Tossing
In this section, we present a composable formalization of (perfectly binding) commitments that can be constructed in the plain model. To this end, we formalize the properties of commitment schemes—correctness, binding, and hiding—each as individual specifications. Thereby, hiding is formalized using the interval-wise guarantees introduced in the previous section. We then apply Blum’s coin-tossing protocol on top of it. While, obviously, the resulting specifications are not sufficient to be used as a CRS, we show that it is unbiased.
5.1 Information-Theoretically Binding Commitments
While UC commitments [5] provide clean and strong guarantees, unfortunately they intrinsically require setup assumptions such as a common reference string. Nevertheless, for many protocols, regular commitments only satisfying the classical game-based properties seem to suffice. This raises the question: can we formalize a weaker yet composable security notion for (non-interactive) commitments?
In Constructive Cryptography, the security of a commitment scheme is formalized using three different constructions [16], for each set of potentially dishonest parties (ignoring the case of both parties being dishonest). Typically, this is presented as one construction parametrized in the set of honest parties, where the ideal specification consists of a filtered resource. That is, for each party \(\mathsf {P}\), a filter \(\phi _\mathsf {P}\) is specified that when connected to the resource limits the honest party’s capabilities. However, there is no fundamental reason for those three construction statements’ specifications to be of some unified type. As a result, we henceforth focus on specifying each property—hiding, binding, and correctness—individually, starting with correctness.
Definition 10
Let \(\varvec{\pi }_{\mathsf {com}}= (\pi _{\mathsf {com}}^\mathtt {A}, \pi _{\mathsf {com}}^\mathtt {B})\) denote a non-interactive commitment protocol where \(\mathtt {A}\) commits a value \(m \in \mathcal {M}\) towards \(\mathtt {B}\). The scheme is said to be (perfectly) correct if

where \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}}\) denotes the commitment resource defined in Fig. 3, and \(\mathsf {Ch}^{\mathtt {A}\rightarrow \mathtt {B}}_1\) and \(\mathsf {Ch}^{\mathtt {A}\rightarrow \mathtt {B}}_2\) denote two single-message communications channelsFootnote 3 from \(\mathtt {A}\) to \(\mathtt {B}\).
Now we proceed to formalize the hiding property. On an intuitive level, (computational) hiding of a non-interactive commitment scheme requires that the commitment string must not reveal any information about the committed value to the receiver \(\mathtt {B}\), until the commitment is opened. Clearly, we can directly apply our notion from Sect. 4 and formalize this using an interval-wise relaxation.
Definition 11
Let \(\varvec{\pi }_{\mathsf {com}}= (\pi _{\mathsf {com}}^\mathtt {A}, \pi _{\mathsf {com}}^\mathtt {B})\) denote a non-interactive commitment protocol. Then, the scheme is said to be (computationally) hiding if

for some simulator \(\sigma _{\mathsf {com}}^\mathtt {B}\) and some computational assumption encoded in \(\epsilon \).
The situation is more challenging with binding. The UC formalization, and analogously \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}}\), requires that the adversary inputs the value to which it commits to in the initial phase, in order to formalize that it then cannot be altered anymore. This, however implies that the simulator must be able to extract the value from the commitment string, fundamentally contradicting the hiding property in the plain model. Since such a formalization is just one (albeit convenient) manner to specify that the value is fixed at the end of the commitment phase, we circumvent this impossibility in another manner. To this end, we consider perfect (or information-theoretically secure) commitments only, where the commitment string uniquely determines the committed value. We leverage this considering a resource \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}, f}\), depicted in Fig. 3, which allows the dishonest \(\mathtt {A}\) to input an arbitrary string x in order to commit to the value \(v=f(x)\). Here, \(f :\{0,1\}^* \rightarrow \mathcal {M} \cup \{\bot \}\) denotes an arbitrary function that maps the commitment string either to a message m, or to \(\bot \) indicating that it is malformed.
Definition 12
Let \(\varvec{\pi }_{\mathsf {com}}= (\pi _{\mathsf {com}}^\mathtt {A}, \pi _{\mathsf {com}}^\mathtt {B})\) denote a non-interactive commitment protocol where \(\mathtt {A}\) commits a value \(m \in \mathcal {M}\) towards \(\mathtt {B}\). Then, the scheme is said to be perfectly binding if there exists an efficient simulator \(\sigma _{\mathsf {com}}^\mathtt {A}\) such that

where \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}, f}\) denotes the extended commitment resource defined in Fig. 3.
As a side note, note that the resource \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}}\) can trivially be expressed as a filtered version of \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}, f}\), where the filter \(\phi _\mathtt {A}\) removes access to the \(\mathtt {commitRaw}\) oracle. That is, we obviously have \(\phi _\mathtt {A}\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}, f} = \mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}}\) for every function f.
Remark 1
Observe that the function f is not necessary efficiently computable. Actually, for a hiding scheme, f cannot be efficiently computable. This, however, does not imply that the overall specification has to contain resources that are not efficiently implementable, as clearly the real-world resource is efficient, and yet corresponds to \(\sigma ^\mathtt {A}\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\mathcal {M}, f}\) for an inefficient f. In other words, the decomposition, containing the inefficient resource, is just one way of describing an overall efficient resource. The specification could, thus, be restricted to consist of only efficient resources, which we did not make explicit here focusing only on the security properties. This is somewhat reminiscent of the solution proposed by Broadnax et al. [3] to deal with inefficient simulators in a manner that retains the expected composition guarantees.
ElGamal commitments. We briefly consider a variant of ElGamal commitments as a concrete instantiation of the above formalized notion. Let \(\mathbb {G} = \langle g\rangle \) denote a cyclic group of order n with generator g.
-
To commit to a message \(m \in \mathbb {G}\), \(((g^a, g^b, m \cdot g^{ab}), (a,b)) \leftarrow {\text {Commit}}(m)\) for \(a,b \in \mathbb {Z}_n\) uniformly at random. That is, the commitment string is \((g^a, g^b, m \cdot g^{ab})\) and the opening value (a, b).
-
 if \(A=g^a\) and \(B=g^b\), and \(\bot \) otherwise.
if \(A=g^a\) and \(B=g^b\), and \(\bot \) otherwise.
Proposition 7
Let \(\varvec{\pi }_{\mathsf {ElG\text {-}com}}\) denote the protocol, i.e., the pair of converters, implementing the aforementioned ElGamal commitment scheme. Then, \(\varvec{\pi }_{\mathsf {ElG\text {-}com}}\) satisfies correctness, hiding (under the DDH assumption), and binding according to Definitions 10 to 12, respectively.
Proof (Sketch)
It is easy to see that the our correctness condition holds. Furthermore, with the simulator \(\sigma _{\mathsf {com}}^\mathtt {B}\) outputting a random triple of group elements as commitment string, hiding holds under the DDH assumption, i.e., for \(\epsilon \) encoding an appropriate reduction to the DDH problem. Finally, consider the function f that maps \((U,V,W) \in \mathbb {G}^3\) to \(W \cdot g^{-{\text {DL}}_g(U) \cdot {\text {DL}}_g(V)}\) and all other bit-strings to \(\bot \). For this function, it is easy to see that a simulator \(\sigma _{\mathsf {com}}^\mathtt {A}\) exists such that the construction that formalizes binding holds. \(\square \)
5.2 Coin-Tossing
In this section, we consider Blum’s simple coin-tossing protocol [2]. The protocol assumes to have a commitment resource from Alice to Bob, and a communication channel in the reverse direction, at its disposal. It then proceeds as follows: Alice chooses \(X \in \{0,1\}\) uniformly at random and commits to it. Once Bob is sure that Alice committed, he chooses \(Y \in \{0,1\}\) uniformly at random and sends it over to Alice (in clear). Finally, Alice opens the commitment and both parties output \(Z = X \oplus Y\).
Clearly, this protocol does not provide fairness—even when instantiated with a UC-secure commitment. This is due to the fact that both parties can always choose to abort the protocol by not responding, and in particular Alice can do so after she has seen the result. When instantiating the commitment with the resource constructed in the last section, one even obtains a weaker resource. Note that this is inherent for our construction being in the plain model, as otherwise it could be used as the bit of a CRS, contradicting well-known impossibility results.
In a nutshell, the resource obtained by our construction guarantees that the output is not biased, but does not exclude that during the opening phase, one of the parties learns some trapdoor allowing it to distinguish it from a uniformly random value. For example, our formalization would allow the resulting bit to be the first bit of a PRG’s output, while leaking the seed during the opening phase. Note that such a coin toss resource is still useful, for instance for lotteries. First, if the resulting bit is just used to determine which party gets some good, then bias-resistance is obviously good enough irrespective of the fact that the parties might be aware that the result is only pseudo-random. Second, in a simple lottery where people’s preferences are obvious, fairness can be achieved by declaring the party that caused the abort to have lost.
The coin-toss resource. The ideal specification is expressed in terms of the resources \(\mathsf {CT}^{\mathtt {A},\mathtt {B}}_{\mathcal {M}}\) and \(\mathsf {CT}^{\mathtt {A},\mathtt {B}}_{\mathcal {M}, f}\), where the former denotes a restricted version of the latter. The resource \(\mathsf {CT}^{\mathtt {A},\mathtt {B}}_{\mathcal {M}}\) initially draws an element \(Z \in \mathcal {M}\) uniformly at random. In order for the coin-toss Z to become available to the parties, \(\mathtt {A}\) has to initiate it, and \(\mathtt {B}\) has to respond afterwards. From this point on, \(\mathtt {A}\) can obtain Z and then decide whether the value should also be released to \(\mathtt {B}\). In the resource \(\mathsf {CT}^{\mathtt {A},\mathtt {B}}_{\mathcal {M}, f}\), \(\mathtt {A}\) furthermore can query once a leakage f(c), of some potentially inefficient function f. A formal definition of the resources can be found in Fig. 4.
The coin-toss resources for coin space \(\mathcal {M}\). In the unfiltered version, Alice additionally has the capability to once obtain a leakage to f(c), where f is a parameter of the resource. Note that neither version provides fairness, as Alice can always chooses to not release the value after having seen it.
The constructions. First, consider correctness. It is easy to see that the following construction holds, i.e., two honest parties actually get to agree on a uniform random bit.
Proposition 8
Let  denote the pair of converters implementing Blum’s protocol. Then, we have
denote the pair of converters implementing Blum’s protocol. Then, we have

and thus

for any commitment scheme \(\varvec{\pi }_{\mathsf {com}}\) satisfying Definition 10 (correctness).
Second, consider the guarantee for an honest initiator \(\mathtt {A}\).
Proposition 9
Let  denote the pair of converters implementing Blum’s protocol. Then, there exists an efficient simulator \(\sigma ^\mathtt {B}_{\mathsf {CT}}\) such that
denote the pair of converters implementing Blum’s protocol. Then, there exists an efficient simulator \(\sigma ^\mathtt {B}_{\mathsf {CT}}\) such that

and thus, for any commitment scheme \(\varvec{\pi }_{\mathsf {com}}\) satisfying Definition 11 (hiding), we have

with  .
.
Proof
Recall that \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\{0,1\}}\) only reveals the value X to Bob after he sent his value Y. Hence, X and Y are independent and with X chosen uniform at random by Alice, implying that \(Z = X \oplus Y\) is a uniform random value. Hence, using the simple simulator \(\sigma ^\mathtt {B}_{\mathsf {CT}}\) that simulates the output of the commitment resource as  , it is easy to see that the construction actually achieves the coin-toss resource perfectly. \(\square \)
, it is easy to see that the construction actually achieves the coin-toss resource perfectly. \(\square \)
Note that this implies that the output Z that Alice obtains looks indistinguishable from a uniform random value until the value is released for the dishonest party. Hence, while it is not guaranteed that the dishonest party does not learn some trapdoor afterwards, the value Z is at least unbiased.
Finally, consider the security guarantees for an honest party \(\mathtt {B}\) against a potentially dishonest party \(\mathtt {A}\). To this end, we turn to the unfiltered resources \(\mathsf {Com}^{\mathtt {A}\rightarrow \mathtt {B}}_{\{0,1\}, f}\) and \(\mathsf {CT}^{\mathtt {A}, \mathtt {B}}_{\{0,1\},f}\), where the latter once allows Alice to obtain f(c) for a c of her choice.
Proposition 10
Let  denote the pair of converters implementing Blum’s protocol. Then, there exists an efficient simulator \(\sigma ^\mathtt {A}_{\mathsf {CT}}\) such that
denote the pair of converters implementing Blum’s protocol. Then, there exists an efficient simulator \(\sigma ^\mathtt {A}_{\mathsf {CT}}\) such that

and thus, for any commitment scheme \(\varvec{\pi }_{\mathsf {com}}\) satisfying Definition 12 (binding), we have

Proof
Consider the real-world system resulting from attaching Bob’s converter only, for some function f. Interacting with this resource, the environment can input a commitment string C at Alice’s interface, then see Bob’s bit Y at Alice’s channel interface, and finally see the resulting bit \(Z = f(C) \oplus Y\) as the output of Bob’s converter. In the following, consider the ideal-world system with the same function f as in the real world. It is now easy to see that a simulator can easily replicate the real-world behavior by getting Z from the resource, querying the leakage-oracle on C getting f(C), and then setting \(Y = Z \oplus f(C)\). \(\square \)
As a final note, observe that formalizing Bob’s security guarantees for the commitment resource in terms of an interval-wise relaxation, rather than introducing the unfiltered resource \(\mathsf {CT}^{\mathtt {A}, \mathtt {B}}_{\{0,1\},f}\), would not work. This is due to the fact that in the real world Y (requiring the additional capabilities to simulate) is output at Alice’s interface before Bob sees Z. Hence, simulating only until Alice sends Y would not give any guarantees on Bob’s output. In summary, this demonstrates Constructive Cryptography’s advantage of being able to consider different types of statements within one (meta-)framework.
6 Conclusion and Future Work
We have demonstrated that considering new types of resource specifications can lead to security notions that are composable, yet do not suffer the artificial impossibilities exhibited by the classical simulation-based definitions. We have introduced a type of specification that formalizes guarantees that hold in a certain time-interval (between two events), which has clean semantics, comes with a natural syntactical composition theorem, and integrates well with the existing Constructive Cryptography framework.
While our novel type of relaxation does not resolve every issue of composable security, we ultimately believe that all (meaningful) security statements can be expressed as an as assumed specification being contained in an ideal one. Further work is, hence, needed to identify additional types of specifications that allow to express more properties—while retaining strong syntactical composition rules and clear semantics.
Notes
- 1.
The analogon to functionalities in the UC framework [4].
- 2.
In CC, the adversary by definition only has access to interfaces statically assigned to him. Hence, adaptive corruptions are modeled by introducing explicit memory and computation resources with an adversarial interface, granting the adversary access once the party is corrupted. For simplicity, we here consider directly leaking key resources instead. Assuming secure erasure, this is equivalent to passive corruptions.
- 3.
That is, a channel that allows the sender to input a single message once. For simplicity, assume that the channel has guaranteed immediate delivery, i.e., whenever the sender has input a message, the receiver can fetch it.
References
Backes, M., Dürmuth, M., Hofheinz, D., Küsters, R.: Conditional reactive simulatability. In: Gollmann, D., Meier, J., Sabelfeld, A. (eds.) ESORICS 2006. LNCS, vol. 4189, pp. 424–443. Springer, Heidelberg (2006). https://doi.org/10.1007/11863908_26
Blum, M.: Coin flipping by telephone a protocol for solving impossible problems. SIGACT News 15(1), 23–27 (1983). https://doi.org/10.1145/1008908.1008911
Broadnax, B., Döttling, N., Hartung, G., Müller-Quade, J., Nagel, M.: Concurrently composable security with shielded super-polynomial simulators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 351–381. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_13
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd IEEE Symposium on Foundations of Computer Science - FOCS 2001, pp. 136–145. IEEE Computer Society (2001)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Krawczyk, H.: Universally composable notions of key exchange and secure channels. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 337–351. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_22
Demay, G., Gaži, P., Maurer, U., Tackmann, B.: Per-session security: password-based cryptography revisited. In: Foley, S.N., Gollmann, D., Snekkenes, E. (eds.) ESORICS 2017. LNCS, vol. 10492, pp. 408–426. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66402-6_24
Hofheinz, D., Matt, C., Maurer, U.: Idealizing identity-based encryption. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 495–520. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_21
Jost, D., Maurer, U.: Overcoming impossibility results in composable security using interval-wise guarantees. Cryptology ePrint Archive, Report 2020/092 (2020). https://eprint.iacr.org/2020/092
Jost, D., Maurer, U., Mularczyk, M.: A unified and composable take on ratcheting. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 180–210. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_7
Kuesters, R., Tuengerthal, M., Rausch, D.: The iitm model: a simple and expressive model for universal composability. Cryptology ePrint Archive, Report 2013/025 (2013). https://eprint.iacr.org/2013/025
Lindell, Y.: General composition and universal composability in secure multiparty computation. J. Cryptology 22(3), 395–428 (2009)
Maurer, U.: Constructive cryptography – a new paradigm for security definitions and proofs. In: Mödersheim, S., Palamidessi, C. (eds.) TOSCA 2011. LNCS, vol. 6993, pp. 33–56. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27375-9_3
Maurer, U.: Indistinguishability of random systems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 110–132. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_8
Maurer, U., Pietrzak, K., Renner, R.: Indistinguishability amplification. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 130–149. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_8
Maurer, U., Renner, R.: Abstract cryptography. In: Innovations in Computer Science - ICS 2011, pp. 1–21. Tsinghua University (2011)
Maurer, U., Renner, R.: From indifferentiability to constructive cryptography (and back). In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 3–24. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_1
Maurer, U., Tackmann, B.: On the soundness of authenticate-then-encrypt: formalizing the malleability of symmetric encryption. In: Keromytis, A.D., Shmatikov, V. (eds.) Proceedings of the 17th ACM Conference on Computer and Communication Security, pp. 505–515. ACM, October 2010
Nielsen, J.B.: Separating random oracle proofs from complexity theoretic proofs: the non-committing encryption case. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 111–126. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_8
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Pfitzmann, B., Waidner, M.: A model for asynchronous reactive systems and its application to secure message transmission. In: Proceedings 2001 IEEE Symposium on Security and Privacy - S&P 2001, pp. 184–200, May 2001. https://doi.org/10.1109/SECPRI.2001.924298
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing, STOC 2004, pp. 242–251. ACM, New York (2004). https://doi.org/10.1145/1007352.1007394
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Jost, D., Maurer, U. (2020). Overcoming Impossibility Results in Composable Security Using Interval-Wise Guarantees. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,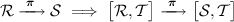 .
. ,
, .
.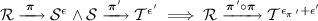 ,
, ,
,


 if
if 
