Abstract
We present a new approach towards constructing round-optimal secure multiparty computation (MPC) protocols against malicious adversaries without trusted setup assumptions. Our approach builds on ideas previously developed in the context of covert multiparty computation [Chandran et al., FOCS’07] even though we do not seek covert security. Using our new approach, we obtain the following results:
-
A five round MPC protocol based on the Decisional Diffie-Hellman (DDH) assumption.
-
A four round MPC protocol based on one-way permutations and sub-exponentially secure DDH. This result is optimal in the number of rounds.
Previously, no four-round MPC protocol for general functions was known and five-round protocols were only known based on indistinguishability obfuscation (and some additional assumptions) [Garg et al., EUROCRYPT’16].
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The notion of secure multiparty computation (MPC) [16, 42] is fundamental in cryptography. Informally speaking, an MPC protocol allows mutually distrusting parties to jointly evaluate a function on their private inputs in such a manner that the protocol execution does not leak anything beyond the output of the function.
A fundamental measure of efficiency in MPC is round complexity, i.e., the number of rounds of communication between the parties. Protocols with smaller round complexity are more desirable so as to minimize the effect of network latency, which in turn decreases the time complexity of the protocol. Indeed, the round complexity of MPC has been extensively studied over the last three decades.
In this work, we study round-optimal MPC against malicious adversaries who may corrupt an arbitrary subset of parties, in the plain model without any trusted setup assumptions. We consider the traditional simultaneous message model for MPC, where in each round of the protocol, each party simultaneously broadcasts a message to the other parties.
A lower bound for this setting was established last year by Garg et al. [14] who proved that three rounds are insufficient for coin-tossing w.r.t. black-box simulation. (Their work builds on [26] who proved the necessity of five rounds for coin-tossing in the unidirectional message model.) In the positive direction, several constant-round MPC protocols were constructed in a long sequence of works, based on a variety of assumptions and techniques (see, e.g., [18, 27, 34, 35, 41]). Garg et al. [14] established an upper bound on the exact round complexity of MPC by constructing a five round protocol based on indistinguishability obfuscation [4, 12] and some additional assumptions.Footnote 1 Their work constitutes the state of the art on this subject.
Our Goals. Presently, no constructions of indistinguishability obfuscation are known from standard assumptions. This motivates the following important question:
Does there exist a five round maliciously-secure MPC protocol for general functions based on standard polynomial-time assumptions?
Furthermore, given the gap between the lower bound (three rounds) and the upper bound (five rounds) established by [14], we ask whether their upper bound is tight:
Does there exist a four round maliciously-secure MPC protocol for general functions?
In this work, we resolve both of these questions in the affirmative.
The Main Barrier. We highlight the main conceptual barrier towards achieving our goals. Garg et al. [14] follow a natural two-step approach to obtain their positive results: in the first step, they construct a four round multiparty coin-tossing protocol. In the next step, they use their coin-tossing protocol to replace the common random string (CRS) in a two-round MPC protocol in the CRS model [11, 31].
We note, however, that this approach, in general, cannot do better than five rounds. Indeed, since at least one of the rounds of the two-round MPC must depend upon the CRS, we can only hope to parallelize its first round with the coin-tossing protocol. Since coin-tossing requires four rounds, this only yields a five round protocol at best.
A New Approach. In this work, we present a new approach towards constructing round-optimal MPC protocols in the plain model. At a high level, our approach implements the classical GMW methodology [16] for constructing maliciously-secure MPC protocols, with a crucial twist, to minimize the number of rounds. This approach is inspired by the beautiful work of Chandran et al. [8] for constructing covert multiparty computation protocols [8, 20, 40].
Recall that the GMW compiler transforms a semi-honest MPC protocol into a maliciously secure one by requiring the parties to prove (using zero-knowledge proofs [17]) that each message in the semi-honest protocol was computed “honestly.” Towards our goal of minimizing round complexity, we cannot afford to prove honest behavior with every round of semi-honest MPC. Therefore, in our approach, the parties prove honest behavior only once.
At first, such an approach may sound completely absurd. If each party is only required to give a single proof of honest behavior, then a malicious adversary may choose to cheat in the first few rounds of the semi-honest MPC protocol. By the time the proof is completed and the honest parties are able to detect cheating, it may already be “too late.” Indeed, the opportunity to cheat in even a single round may be sufficient for a malicious adversary to completely break the security of a semi-honest protocol. Therefore, it is not at all clear why such an approach can be implemented in a secure manner.
In order to tackle this problem, we design a “special-purpose” semi-honest MPC protocol that remains partially immune to malicious behavior before the last round of the protocol. Specifically, in such a protocol, an adversary can influence the protocol outcome but not learn any private information by behaving maliciously before the last round. We then “shield” the last round from being revealed to the adversary until it has proven honest behavior for all of the preceding rounds. A single proof suffices to accomplish this task. By parallelizing this proof with the semi-honest MPC, we are able to minimize the round complexity.
We note that the above idea of delaying the proof of honest behavior to the end of the computation was first developed in [8]. While they developed this technique to achieve covert security (namely, hiding protocol participation from other players), we use it in our setting to minimize round complexity.
1.1 Our Results
We present a new approach for constructing round-efficient MPC protocols that are secure against malicious adversaries in the plain model. Using this approach, we are able to achieve both of our aforementioned goals.
I. Robust Semi-honest MPC. As a first step towards obtaining our results for maliciously-secure MPC, we construct a four round robust semi-honest MPC protocol that remains partially immune to malicious behavior. In this protocol, at the end of the first three rounds of computation, each party receives a secret share of the function output. In the last round, the parties simply exchange their shares to reconstruct the output. The key security property of this protocol is that if the adversary cheats in the first three rounds, then it can only influence the function output, but not learn any private information.
We construct such an MPC scheme for general functions assuming the existence of low-depth pseudorandom generators (PRGs) and a two-round “covert” oblivious transfer (OT) protocol [40].Footnote 2 Both of these primitives can be instantiated from the Decisional Diffie-Hellman (DDH) assumption.
Theorem 1
Assuming DDH, there exists a four round robust semi-honest MPC protocol for general functions.
The above result may be of independent interest.
II. Maliciously-secure MPC. Using Theorem 1, we next construct maliciously-secure MPC protocols in the plain model.
Our first result is a five round MPC protocol based on any four-round robust semi-honest MPC, injective one-way functions and collision-resistant hash functions (CRHFs). Since injective one-way functions and CRHFs can be built from Discrete Log, we obtain the following result:
Theorem 2
(Five Rounds). Assuming DDH, there exists a five round maliciously-secure MPC protocol for computing general functions.
We next modify our five round protocol to obtain a four round protocol, albeit using sub-exponential hardness. The security of our construction uses complexity leveraging between multiple primitives.
Theorem 3
(Four Rounds). Assuming one-way permutations and sub-exponentially secure DDH, there exists a four round maliciously-secure MPC protocol for computing general functions.
1.2 Our Techniques
As discussed earlier, the approach of Garg et al. [14] for constructing maliciously-secure MPC protocols is unsuitable for achieving our goals. Therefore, we develop a new approach for constructing round-efficient MPC against malicious adversaries.
At a high-level, our approach implements the GMW paradigm for constructing maliciously-secure MPC protocols, with a crucial twist. Recall that the GMW paradigm transforms a semi-honest MPC protocol into a maliciously secure one using the following three steps: (1) first, the parties commit to their inputs and random tapes. (2) Next, the parties perform coin-tossing to establish an unbiased random tape for each party. (3) Finally, the parties run the semi-honest MPC protocol where along with every message, each party also gives zero-knowledge proof of “honest” behavior consistent with the committed input and random tape.
Both steps (2) and (3) above introduce additional rounds of interaction, and constitute the main bottleneck towards constructing round-optimal MPC.
Main Ideas. Towards this, we develop two key modifications to the GMW compiler:
-
1.
“One-shot” proof: Instead of requiring the parties to give a proof of honest behavior in each round of the underlying semi-honest protocol, we use a “delayed verification” technique where the parties prove honest behavior only once, towards the end of the protocol. As we explain below, this allows us to limit the overhead of additional rounds introduced by zero-knowledge proofs in the GMW compiler.
The idea of delayed verification was previously developed in the work of Chandran et. al. [8]. Interestingly, while they used this technique to achieve security in the setting of covert computation [8, 40], we use this technique to minimize the round complexity of our protocol.
-
2.
No coin tossing: Second, we eliminate the coin-tossing step (i.e., step 2). Note that by removing coin-tossing, we implicitly allow the adversarial parties to potentially use “bad” randomness in the protocol. To ensure security in this scenario, we will use a special semi-honest MPC protocol that is secure against bad randomness. This idea has previously been used in many works (see, e.g., [3, 31]).
We now elaborate on the first step, which constitutes the conceptual core of our work. We consider semi-honest MPC protocols with a specific structure consisting of two phases: (a) Computation phase: in the first phase of the protocol, the parties compute the function such that each party obtains a secret-share of the output. (b) Output phase: In the second phase, the parties exchange their output shares with each other to compute the final output. This phase consists of only one round and is deterministic. Note that standard MPC protocols such as [16] follow this structure.
At a high-level, we implement our delayed verification strategy as follows: the parties first run the computation phase of the semi-honest protocol “as is” without giving any proofs. At the end of this phase, each party gives a single proof that it behaved honestly throughout the computation phase (using the committed input and random tape). If all the proofs verify, then the parties execute the output phase.
Right away, one may notice a glaring problem in the above approach. If the computation phase is executed without any proof of honest behavior, the adversary may behave maliciously in this phase and potentially learn the honest party inputs even before the output phase begins! Indeed, standard semi-honest MPC protocols do not guarantee security in such a setting.
To combat this problem, we develop a special purpose semi-honest MPC protocol that remains “partially immune” to malicious behavior. Specifically, such a protocol maintains privacy against malicious adversaries until the end of the computation phase. However, output correctness is not guaranteed if the adversary behaved maliciously in the computation phase. We refer to such an MPC protocol as robust semi-honest MPC. Later, we describe a four-round construction of robust semi-honest MPC where the first three rounds correspond to the computation phase and the last round constitutes the output phase.
Note that the robustness property as described above perfectly suits our requirements because in our compiled protocol, the output phase is executed only after each party has proven that it behaved honestly during the computation phase. This ensures full security of our compiled protocol.
A New Template for Malicious MPC. Putting the above ideas together, we obtain the following new template for maliciously-secure MPC:
-
First, each party commits to its input and randomness using both a three-round extractable commitment schemeFootnote 3, and a non-interactive commitment scheme. In parallel, the parties also execute the computation phase of a four-round robust semi-honest MPC.
-
Next, each party proves to every other party that it behaved honestly during the first three rounds.
-
Finally, the parties execute the output phase of the robust semi-honest MPC and once again prove that their message is honestly computed.
In order to obtain a five round protocol from this template, we need to parallelize the proofs with the other protocol messages. For this purpose, we use delayed-input proofs [29] where the instance is only required in the last round.Footnote 4 In particular, we use four-round delayed input zero-knowledge (ZK) proofs whose first three messages are executed in parallel with the first three rounds of the robust semi-honest MPC. This yields us a five round protocol.
We remark that during simulation, our simulator is able to extract the adversary’s input only at the end of the third round. This means that we need to simulate the first three rounds of the robust semi-honest MPC without knowledge of the adversary’s input (or the function output). Our robust semi-honest MPC satisfies this property; namely, the simulator for our robust semi-honest MPC needs the adversary’s input and randomness (and the function output) only to simulate the output phase.
Four Rounds: Main Ideas. We next turn to the problem of constructing four-round MPC. At first, it is not clear how to obtain a four round protocol using the above template. Indeed, as argued earlier, we cannot afford to execute the output phase without verifying that the parties behaved honestly during the computation phase. In the above template, the output phase is executed after this verification is completed. Since three-round zero-knowledge proofs with polynomial-time simulation are not known presently, the verification process in the above protocol requires four rounds. Therefore, it may seem that that we are limited to a five round protocol.
Towards that, we note that our robust semi-honest MPC (described later) satisfies the following property: in order to simulate the view of the adversary (w.r.t. the correct output), the simulator only needs to “cheat” in the output phase (i.e., the last round). In particular, the simulation of the computation phase can be done “honestly” using random inputs for the honest parties. In this case, we do not need full-fledged ZK proofs to establish honest behavior in the computation phase; instead, we only need strong witness indistinguishable (WI) proofs. Recall that in a strong WI proof system, for any two indistinguishable instance distributions \(D_1\) and \(D_2\), a proof for \(x_1\leftarrow D_1\) using a witness \(w_1\) is indistinguishable from a proof for \(x_2\leftarrow D_2\) using a witness \(w_2\). This suffices for us because using strong WI, we can switch from an honest execution of the computation phase using the real inputs of the honest parties to another honest execution of the computation phase using random inputs for the honest parties.
Recently, Jain et al. [25] constructed three-round delayed-input strong WI proofs of knowledge from the DDH assumption. However, their proof system only guarantees strong WI property if the entire statement is chosen by the prover in the last round. In our case, this is unfortunately not true, and hence we cannot use their construction. Therefore, we take a different route, albeit at the cost of sub-exponential hardness assumptions. Specifically, we observe that by relying upon sub-exponential hardness, we can easily construct a three-round (delayed-input) strong WI argument by combining any three-round (delayed-input) WI proof of knowledge with a one or two-message “trapdoor phase” in our simultaneous message setting. For example, let f be a one-way permutation. The trapdoor phase can be implemented by having the verifier send \(y=f(x)\) for a random x in parallel with the first prover message. The statement of the WI proof of knowledge is changed to: either the original statement is true or the prover knows x.
Now, by running in exponential time in the hybrids, we can break the one-way permutation to recover x and then prove knowledge of x. This allows us to switch from honest execution of the computation phase using the real inputs of the honest parties to another honest execution using random inputs. After this switch, we can go back to proving the honest statement which can be done in polynomial time. This ensures that our final simulator is also polynomial time.
Handling Non-malleability Issues. So far, we ignored non-malleability related issues in our discussion. However, as noted in many prior works, zero-knowledge proofs with standard soundness guarantee do not suffice in the setting of constant-round MPC. Indeed, since proofs are being executed in parallel, we need to ensure that an adversary’s proofs remain sound even when the honest party’s proofs are being simulated [39].
We handle such malleability issues by using the techniques developed in a large body of prior works. In our five round MPC protocol, we use a slight variant of the four-round non-malleable zero-knowledge (NMZK) argument of [9] to ensure that adversary’s proofs remain sound even during simulation.Footnote 5 We make non-black-box use of their protocol in our security proof. More specifically, following prior works such as [5, 13, 19, 21], we establish a “soundness lemma” to ensure that the adversary is behaving honestly across the hybrids. We use the extractability property of the non-malleable commitment used inside the non-malleable zero-knowledge argument to prove this property.
In our four round protocol, we use the above NMZK to prove honest behavior in the output phase. In order to prove honest behavior in the computation phase, we use a slightly modified version of the strong WI argument system described above which additionally uses either a three-round [22] or two-round [28] non-malleable commitment scheme with extractability to achieve the desired non-malleability properties. Unlike the five round construction, here, we rely upon complexity leveraging in several of the hybrids to argue the “soundness lemma” as well as to tackle some delicate rewinding-related issues that are commonplace in such proofs.Footnote 6 We refer the reader to the technical sections for details.
Robust Semi-honest MPC. We now briefly describe the high-level ideas in our four-round construction of robust semi-honest MPC for general functionalities. Towards this, we note that it suffices to achieve a simpler goal of constructing robust semi-honest MPC for a restricted class of functionalities, namely, for computing randomized encodings.Footnote 7 That is, in order to construct a robust MPC for a \(n\)-party functionality \(F\), it suffices to construct a robust MPC for a \(n\)-functionality \(F_{rnd}\) that takes as input \((x_1,r_1;\cdots ;x_{n},r_{n})\) and outputs a randomized encoding of \(F(x_1,\ldots ,x_{n})\) using randomness \(r_1 \oplus \cdots \oplus r_{n}\). This is because all the parties can jointly execute the protocol for \(F_{rnd}\) to obtain the randomized encoding. Each party can then individually execute the decoding algorithm of the randomized encoding to recover the output \(F(x_1,\ldots ,x_{n})\). Note that this transformation preserves round complexity.
To construct a robust semi-honest \(n\)-party protocol for \(F_{rnd}\), we consider a specific type of randomized encoding defined in [2]. In particular, they construct a degree 3 randomizing polynomialsFootnote 8 for arbitrary functionalities based on low-depth pseudorandom generators. In their construction, every output bit of the encoding can be computed by a degree 3 polynomial on the input and the randomness. Hence, we further break down the goal of constructing a protocol for \(F_{rnd}\) into the following steps:
-
Step 1: Construct a robust semi-honest MPC 3-party protocol for computing degree 3 terms. In particular, at the end of the protocol, every party who participated in the protocol get a secret share \(x_1x_2x_3\), where \(x_{q}\) is the \(q^{th}\) party’s input for \(q \in \{1,2,3\}\). The randomness for the secret sharing comes from the parties in the protocol.
-
Step 2: Using Step 1, construct a robust semi-honest MPC protocol to compute degree 3 polynomials.
-
Step 3: Using Step 2, construct a robust semi-honest MPC protocol for \(F_{rnd}\).
Steps 2 and 3 can be achieved using standard transformations and these transformations are round preserving. Thus, it suffices to achieve Step 1 in four rounds. Suppose \(P_{1},P_{2}\) and \(P_{3}\) participate in the protocol. Roughly, the protocol proceeds as follows: \(P_{1}\) and \(P_{2}\) perform a two message covert OT protocol to receive a share of \(x_1x_2\). Then, \(P_{1}\) and \(P_{3}\) perform a two message OT protocol to receive a share of \(x_1x_2x_3\). We need to do more work to ensure that at the end, all of them have shares of \(x_1x_2x_3\). Further, the robustness guarantee is argued using the covert security of the OT protocol. We refer the reader to the technical sections for more details.
1.3 Concurrent Work
In a concurrent and independent work, Brakerski et al. [7] construct a maliciously-secure 4-round MPC protocol based on the sub-exponential hardness of the Learning with Errors (LWE) problem and on the adaptive commitments of [33]. Their approach is very different from ours, most notably in the initial step, in that they construct and use a 3-round protocol against semi-malicious adversaries from LWE, while we construct and use a robust semi-honest MPC protocol from DDH.
1.4 Related Work
The study of constant-round protocols for MPC was initiated by Beaver et al. [6]. Their constructed constant-round MPC protocols in the presence of honest majority. Subsequently, a long sequence of works constructed constant-round MPC protocols against dishonest majority based on a variety of assumptions and techniques (see, e.g., [18, 27, 34, 35, 41]). Very recently, Garg et al. [14] constructed five round MPC using indistinguishability obfuscation and three-round parallel non-malleable commitments. They also construct a six-round MPC protocol using learning with errors (LWE) assumption and three-round parallel non-malleable commitments. All of these results are in the plain model where no trusted setup assumptions are available.
Asharov et al. [3] constructed three round MPC protocols in the CRS model. Subsequently, two-round MPC protocols in the CRS model were constructed by Garg et al. [11] using indistinguishability obfuscation, and by Mukherjee and Wichs [31] using LWE assumption.
1.5 Full Version
Due to space constraints, much of the details of the security proofs for our constructions are omitted from this manuscript. The full version of the paper is available at [1].
2 Definitions
We denote n to be the security parameter. Consider two distributions \(\mathcal {D}_0\) and \(\mathcal {D}_1\). We denote \(\mathcal {D}_0 \approx _{c} \mathcal {D}_1\) if \(\mathcal {D}_0\) and \(\mathcal {D}_1\) are computationally indistinguishable.
2.1 Oblivious Transfer
We recall the notion of oblivious transfer [10, 37] below. We require that the oblivious transfer protocol satisfies covert security [8, 20, 40]. Intuitively, we require that the receiver’s messages are computationally indistinguishable from a uniform distribution to a malicious sender. Similarly, we require that the sender’s messages are computationally indistinguishable from a uniform distribution to a malicious receiver.
Definition 1
(Covert Oblivious Transfer). A 1-out-of-2 oblivious transfer (OT) protocol \(\mathsf {OT}\) is a two party protocol between a sender and a receiver. A sender has two input bits \((b_0,b_1)\) and the receiver has a choice bit c. At the end of the protocol, the receiver receives an output bit \(b'\). We denote this process by \(b' \leftarrow \langle \mathsf {Sen}(b_0,b_1),\mathsf {Rec}(c) \rangle \).
We require that an OT protocol satisfies the following properties:
-
Correctness: For every \(b_0,b_1,c \in \{0,1\}\), we have:
$$\mathsf {Pr}[b_c \leftarrow \langle \mathsf {Sen}(b_0,b_1),\mathsf {Rec}(c) \rangle ] = 1$$ -
Covert security against adversarial senders: For all PPT senders \(\mathsf {Sen}^*\), we require that the honest receiver’s messages are computationally indistinguishable from uniform distribution.
-
Covert security against adversarial receivers: Suppose the input of the sender \((b_0,b_1)\) is sampled from a distribution on \(\{0,1\}^2\). For all PPT receivers \(\mathsf {Rec}^*\), we require that the honest sender’s messages (computed as a function of \((b_0,b_1)\)) are computationally indistinguishable from uniform distribution.
An oblivious transfer protocol satisfying the above definition was constructed in [40] using [32].
Theorem 4
[40]. Assuming decisional Diffie Helman assumption, there exists a two message 1-out-of-2 covert oblivious transfer protocol.
We note that for our constructions, it actually suffices if the OT protocol achieves indistinguishability security against malicious senders and receivers. (This property is satisfied by [32].) The covertness property helps to simplify the proof of our robust semi-honest MPC.
2.2 Randomizing Polynomials
We first recall the definition of randomizing polynomials [2, 24]. Instead of considering the standard form of randomizing polynomials consisting of encode and decode algorithms, we instead consider a decomposable version where the circuit is first encoded as polynomials and decode algorithm gets as input evaluations of polynomials on input and randomness.
Definition 2
(Randomizing Polynomials). A randomizing polynomials scheme \(\mathsf {RP}=(\mathsf {CktE},\mathsf {D})\) for a family of circuits \(\mathcal {C}\) has the following syntax:
-
Encoding, \(\mathsf {CktE}(C)\): On input circuit \(C \in \mathcal {C}\), input x, it outputs polynomials \(p_1,\ldots ,p_{m}\).
-
Decoding, \(\mathsf {D}(p_1(x;r),\ldots ,p_m(x;r))\): On input evaluations of polynomials \(p_1(x;r), \ldots ,p_m(x;r)\), it outputs the decoded value \(\alpha \).
\(\mathsf {RP}\) is required to satisfy the following properties:
-
Correctness: For every security parameter \(n \in \mathbb {N}\), circuit C and input x, \(C(x)=\mathsf {D}(p_1(x;r),\ldots ,p_m(x;r))\), where (i) \((p_1,\ldots ,p_m) \leftarrow \mathsf {CktE}(C)\), (ii) r is randomness sampled from uniform distribution.
-
Efficiency: The typical efficiency we require is that the degree of the polynomials \(\{p_i\}\) should be significantly smaller than the degree of the circuit C, where \((p_1,\ldots ,p_m) \leftarrow \mathsf {CktE}(C)\).
-
Security: For every PPT adversary \(\mathcal {A}\), for large enough security parameter \(n \in \mathbb {N}\), circuit C and input x, there exists a simulator \(\mathsf {Sim}\) such that:
$$\left\{ (p_1(x;r),\ldots ,p_m(x;r)) \right\} \approx _c \left\{ \mathsf {Sim}(1^{n},1^{|C|},C(x))\right\} ,$$where (i) \((p_1,\ldots ,p_m) \leftarrow \mathsf {CktE}(C)\), (ii) r is randomness sampled from uniform distribution.
We define the degree of randomizing polynomials to be \(\max _{C \in \mathcal {C}}\{\mathrm {deg}(p_i): \ (p_1,\ldots ,p_m) \leftarrow \mathsf {CktE}(C \in \mathcal {C})\}\).
We have the following theorem from [2].
Theorem 5
[2]. Assuming the existence of pseudorandom generators in \(\oplus \mathrm {L}/Poly\) for all polynomial-time computable functions.
2.3 Non-malleable Commitments
Let \(\varPi = \langle C, R\rangle \) be a statistically binding commitment scheme. Consider MiM adversaries that are participating in one left and one right sessions in which k commitments take place. We compare between a MiM and a simulated execution. In the MiM execution, the adversary \(\mathcal {A}\), with auxiliary information z, is participating in one left and one right sessions. In the left session, the MiM adversary interacts with C receiving commitments to value m using identities \(\mathtt{id}\) of its choice. In the right session \(\mathcal {A}\) interacts with R, attempting to commit to a related value \(\tilde{m}\) again using identities \(\tilde{\mathtt{id}}\) of its choice. If any the right commitment is invalid, or undefined, its value is set to \(\perp \). If \(\tilde{\mathtt{id}} = \mathtt{id}\), set \(\tilde{m} = \perp \) (i.e., any commitment where the adversary uses the same identity as that of honest senders is considered invalid). Let \( \textsf {mim}_{\varPi }^{\mathcal {A},m}(z)\) denote the random variable that describes the values \(\tilde{m}\) and the view of \(\mathcal {A}\), in the above experiment.
In the simulated execution, an efficient simulator \(\mathsf{Sim}\) directly interacts with R. Let \(\textsf {sim}_{\varPi }^\mathsf{Sim}(1^n,z) \) denote the random variable describing the value \(\tilde{m}\) committed by \(\mathsf{Sim}\), and the output view of \(\mathsf{Sim}\); whenever the view contains the same identity as that identity of the left session, \(\tilde{m}\) is set to \(\perp \).
Definition 3
(non-malleable commitment scheme). A commitment scheme is non-malleable with respect to commitment if, for every \(\mathsf{PPT}\) parallel MiM adversary \(\mathcal {A}\), there exists a \(\mathsf{PPT}\) simulator \(\mathsf{Sim}\) such that for all m the following ensembles are computationally indistinguishable:
For our construction, we will require that the non-malleable commitments are public coin and extractable. Four round non-malleable commitments based on CRHFs satisfying both the conditions are described in [23]. Similarly, three round non-malleable commitments based on quasi-polynomial injective OWFs satisfying both conditions are described in [22]. Two round (private coin) non-malleable commitments, with respect to commitment, are based on sub-exponential hardness of DDH [28]. Additionally, two round non-interactive concurrent non-malleable commitments can be based on time-lock puzzles [30].
Binding Property of the Commitments. For convenience, we assume that the first message sent by the committer in the four round non-malleable commitment scheme is statistically binding. Thus, the second message in the scheme is statistically binding. The non-malleable commitment scheme in [9] satisfies this property. But importantly, with minor modifications our proofs go through even without this assumption.
2.4 Delayed-Input Non-malleable Zero Knowledge
Let \(\varPi _\mathsf{nmzk}= \langle P, V\rangle \) be a delayed-input interactive argument system for an NP-language L with witness relation \(\mathsf{Rel}_L\). Consider a PPT MiM adversary \(\mathcal {A}\) that is simultaneously participating in one left session and one right session. Before the execution starts, both P, V and \(\mathcal {A}\) receive as a common input the security parameter n, and \(\mathcal {A}\) receives as auxiliary input \(z \in \lbrace 0,1\rbrace ^*\).
In the left session \(\mathcal {A}\) interacts with P using identity \(\mathtt{id}\) of his choice. In the right session, \(\mathcal {A}\) interacts with V, using identity \(\widetilde{\mathtt{id}}\) of his choice.
In the left session, before the last round of the protocol, P gets the statement x. Also, in the right session \(\mathcal {A}\), during the last round of the protocol selects the statement \(\tilde{x}\) to be proved and sends it to V. Let \(\mathsf {View}^\mathcal {A}(1^n,z)\) denote a random variable that describes the view of \(\mathcal {A}\) in the above experiment.
Definition 4
(Delayed-input NMZK). A delayed-input argument system \(\varPi _\mathsf{nmzk}= \langle P, V\rangle \) for \(\mathsf NP\)-language L with witness relation \(\mathsf Rel_L\) is Non-Malleable Zero Knowledge (NMZK) if for any MiM adversary \(\mathcal {A}\) that participates in one left session and one right session, there exists a \(\mathsf{PPT}\) machine \(\mathsf{Sim}(1^n,z)\) such that
-
1.
The probability ensembles \(\lbrace \mathsf{Sim}^1(1^n,z)\rbrace _{n\in \mathbb {N}, z \in \lbrace 0,1\rbrace ^*}\) and
\(\lbrace \mathsf {View}^\mathcal {A}(1^n,z)\rbrace _{\lambda \in \mathbb {N}, z \in \lbrace 0,1\rbrace ^*}\) are computationally indistinguishable over n, where \(\mathsf{Sim}^1(1^n,z)\) denotes the first output of \(\mathsf{Sim}(1^n,z)\).
-
2.
Let \(z \in \lbrace 0,1\rbrace ^*\) and let \((\mathsf {View},\tilde{w})\) denote the output of \(\mathsf{Sim}(1^n,z)\). Let \(\tilde{x}\) be the right-session statement appearing in \(\mathsf View\) and let \(\mathtt{id}\) and \(\tilde{\mathtt{id}}\) be the identities of the left and right sessions appearing in \(\mathsf View\). If the right session is accepting and \(\mathtt{id}\ne \tilde{\mathtt{id}}\), then \(\mathsf{Rel_L}(\tilde{x},\tilde{w})=1\).
The above definition, is easily extended to parallel NMZK, where the adversary interacts with a polynomially bounded sessions on the left and right in parallel.
For our constructions, we shall use a slight variant of the 4-round NMZK protocol in [9]. The protocol is secure assuming CRFHs, and can thus be instantiated from DDH, and we refer the reader to their paper for a description of the protocol. In their protocol, in the honest setting, the internal WI proof system proves that the non-malleable commitment contains the witness to the NMZK languageFootnote 9, or that it knows the trapdoor. Instead in our variant, we modify the internal proof system to prove that either the NMZK instance is true or the non-malleable commitment contains the trapdoor. We give a detailed discussion in the full version of our paper. Additionally, we note that their protocol is also parallel ZK since we can extract trapdoors of multiple executions in parallel.
2.5 Extractable Commitment Scheme
We will also use a simple challenge-response based extractable statistically-binding string commitment scheme \({\langle C,R\rangle }\) that has been used in several prior works, most notably [36, 38]. We note that in contrast to [36] where a multi-slot protocol was used, here (similar to [38]), we only need a one-slot protocol.
Protocol \({\langle C,R\rangle }\). Let \(\mathsf{com}(\cdot )\) denote the commitment function of a non-interactive perfectly binding string commitment scheme which requires the assumption of injective one-way functions for its construction. Let n denote the security parameter. The commitment scheme \({\langle C,R\rangle }\) is described as follows.
Commit Phase:
-
1.
To commit to a string \(\texttt {str}\), C chooses \(k=\omega (\log (n))\) independent random pairs \(\{\alpha _{i}^0,\alpha _{i}^1\}_{i=1}^{k}\) of strings such that \(\forall i\in [k]\), \(\alpha _i^0\oplus \alpha _i^1=\texttt {str}\); and commits to all of them to R using \(\mathsf{com}\). Let \(B\leftarrow \mathsf{com}(\texttt {str})\), and \(A_i^{0}\leftarrow \mathsf{com}(\alpha _i^{0})\), \(A_i^{1}\leftarrow \mathsf{com}(\alpha _i^{1})\) for every \(i\in [k]\).
-
2.
R sends k uniformly random bits \(v_1,\ldots ,v_n\).
-
3.
For every \(i\in [k]\), if \(v_i=0\), C opens \(A_i^{0}\), otherwise it opens \(A_i^{1}\) to R by sending the appropriate decommitment information.
Open Phase: C opens all the commitments by sending the decommitment information for each one of them.
For our construction, we require a modified extractor for the extractable commitment scheme. The standard extractor returns the value str that was committed to in the scheme. Instead, we require that the extractor return i, and the openings of \(A^0_i\) and \(A^1_i\). This extractor can be constructed easily, akin to the standard extractor for the extractable commitment scheme.
This completes the description of \({\langle C,R\rangle }\).
“Rewinding secure” Commitment Scheme. Due to technical reasons, we will also use a minor variant, denoted \(\langle C',R' \rangle \), of the above commitment scheme which will be rewinding secure. Protocol \(\langle C',R' \rangle \) is the same as \({\langle C,R\rangle }\), except that for a given receiver challenge string, the committer does not “open” the commitments, but instead simply reveals the appropriate committed values (without revealing the randomness used to create the corresponding commitments). More specifically, in protocol \(\langle C',R' \rangle \), on receiving a challenge string \(v_1,\ldots ,v_n\) from the receiver, the committer uses the following strategy: for every \(i\in [k]\), if \(v_i=0\), \(C'\) sends \(\alpha _i^{0}\), otherwise it sends \(\alpha _i^{1}\) to \(R'\). Note that \(C'\) does not reveal the decommitment values associated with the revealed shares.
The scheme is rewinding secure because we can respond to queries from the adversary (for the commitment scheme) when we need to rewind it, and the commitment scheme is exposed to an external challenger. This follows from the fact that we can send random messages in the third round when the adversary makes a different second round query.
When we use \(\langle C',R' \rangle \) in our main construction, we will require the committer \(C'\) to prove the “correctness” of the values (i.e., the secret shares) it reveals in the last step of the commitment protocol. In fact, due to technical reasons, we will also require the committer to prove that the commitments that it sent in the first step are “well-formed”. Below we formalize both these properties in the form of a validity condition for the commit phase.
Proving Validity of the Commit Phase. We say that commit phase between \(C'\) and \(R'\) is well formed with respect to a value \(\hat{\texttt {str}}\) if there exist values \(\{\hat{\alpha }^0_{i}, \hat{\alpha }^1_{i}\}_{i=1}^k\) such that:
-
1.
For all \(i\in [k]\), \({\hat{\alpha }}^0_{i}\oplus {\hat{\alpha }}^1_{i}=\hat{\texttt {str}}\), and
-
2.
Commitments B, \(\{A^0_{i},A^1_{i}\}_{i=1}^k\) can be decommitted to \(\hat{\texttt {str}}\), \(\{\hat{\alpha }^0_{i}, \hat{\alpha }^1_{i}\}_{i=1}^k\) respectively.
-
3.
Let \(\bar{\alpha }_{1}^{v_{1}},\ldots ,\bar{\alpha }_{k}^{v_{k}}\) denote the secret shares revealed by C in the commit phase. Then, for all \(i\in [k]\), \(\bar{\alpha }_{i}^{v_{i}}=\hat{\alpha }_{i}^{v_{i}}\).
We state a simple lemma below, that states that \(\exists \) an extractor E that extracts the correct committed value with overwhelming probability if the commitment is well formed. This lemma is implicit from [36, 38].
Lemma 1
If the validity condition for the commitment protocol holds, then E fails to extract the committed value with only negligible probability.
3 Robust Semi-honest MPC
We consider semi-honest secure multi-party computation protocols that satisfy an additional robustness property. Intuitively the property says that, except the final round, the messages of honest parties reveal no information about their inputs even if the adversarial parties behave maliciously.
Definition 5
Let F be an \(n\)-party functionality. Let \(\mathcal {A}=(\mathcal {A}^1,\mathcal {A}^2)\) represent a PPT algorithm controlling a set of parties \(S \subseteq [n]\). For a t-round protocol computing F, we let \(\mathsf{RealExec}^{\mathcal {A}^1}_{(t-1)}({\varvec{x}}, z)\) denote the view of \(\mathcal {A}^1\) during the first \(t-1\) rounds in the real execution of the protocol on input \({\varvec{x}} = (x_1,\cdots ,x_n)\) and auxiliary input z. We require that at the end of the first \(t-1\) rounds in the real protocol, \(\mathcal {A}^1\) outputs \(\mathsf {state}\) and \((\mathsf{inp, rand})\) on a special tape where either \((\mathsf{inp, rand}) = (\perp , \perp )\) (if \(\mathcal {A}^1\) behaved maliciously) or \( (\mathsf{inp, rand}) = \left( \{\widehat{x_i}\}_{i \in S},\{\widehat{r_i}\}_{i \in S}\right) \) which is consistent with the honest behavior for \(\mathsf{RealExec}_{(t-1)}\) (first \(t-1\) rounds).
A protocol is said to be a “robust” secure multiparty computation protocol for F if for every PPT adversary \(\mathcal {A}=(\mathcal {A}^1,\mathcal {A}^2)\) controlling a set of parties S in the real world, where \(\mathcal {A}^2\) is semi-honest, there exists a PPT simulator \(\mathsf {Sim}=(\mathsf {Sim}^1,\mathsf {Sim}^2)\) such that for every initial input vector \({\varvec{x}}\), every auxiliary input z
-
If \((\mathsf{inp, rand}) \ne (\perp , \perp )\), then:
$$\begin{aligned} \left( \mathsf{RealExec}_{(t-1)}^{\mathcal {A}^1}({\varvec{x}}, z),\right.&\left. \mathsf{RealExec}_{t}^{\mathcal {A}^2}({\varvec{x}}, \mathsf {state})\right) \\&\approx _c \left( \mathsf{RealExec}_{(t-1)}^{\mathcal {A}^1}({\varvec{x}}, z), ~\mathsf {Sim}^2(\{\widehat{x_i}\}_{i \in S},\{\widehat{r_i}\}_{i \in S}, y, \mathsf {state})\right) \\&\approx _c \left( \mathsf {Sim}^1(z),~ \mathsf {Sim}^2\left( \{\widehat{x_i}\}_{i \in S},\{\widehat{r_i}\}_{i \in S}, y, \mathsf {state}\right) \right) . \end{aligned}$$Here \(y=F(\widehat{x_1},\ldots ,\widehat{x_n})\), where \(\widehat{x_i}=x_i\) for \(i \notin S\). And \(\mathsf{RealExec}_{t}^{\mathcal {A}^2}({\varvec{x}}, \mathsf {state})\) is the view of adversary \(\mathcal {A}^2\) in the \(t^{th}\) round of the real protocol.
-
Else,
$$ \mathsf{RealExec}_{(t-1)}^{\mathcal {A}^1}({\varvec{x}}, z) \approx _c \mathsf {Sim}^1(z). $$
Note that, in general, a semi-honest MPC protocol may not satisfy this property. Below, we construct a four-round semi-honest MPC protocol with robustness property.
3.1 Four Round Robust Semi-honest MPC
We first describe the tools required for our construction. We require,
-
Two message 1-out-of-2 covert oblivious transfer protocol. Denote this by \(\mathsf {OT}\).
-
Degree 3 randomizing polynomials for arbitrary polynomial sized circuits. Denote this by \(\mathsf {RP}=(\mathsf {CktE},\mathsf {D})\).
Both the tools mentioned above can be instantiated from DDH.
Construction. Our goal is to construct an \(n\)-party MPC protocol \(\varPi _{\mathsf {sh}}^{F}\) secure against semi-honest adversaries for an \(n\)-party functionality \(F\). Moreover, we show that \(\varPi _{\mathsf {sh}}^{F}\) satisfies Robust property (Definition 5). We employ the following steps:
-
Step I: We first construct an 3-party semi-honest MPC protocol \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) for the functionality \(\mathsf {3MULT}\) defined below. This protocol is a three round protocol. However, we view this as a four round protocol (with the last round being empty) – the reason behind doing this is because this protocol will be used as a sub-protocol in the next steps and in the proof, the programming of the simulator occurs only in the fourth round.
$$ \mathsf {3MULT}((x_1,r_1);(x_2,r_2);(x_3)) \text { outputs } (r_1;\ r_2;\ x_1x_2x_3+r_1+r_2) $$ -
Step II: We use \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) to construct an \(n\)-party semi-honest MPC protocol \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) for the functionality \(\mathsf {3POLY}\{p\}\) defined below, where p is a degree 3 polynomial in \(\mathbb {F}_2[\mathbf {y}_1,\ldots ,\mathbf {y}_{N}]\). This protocol is a four round protocol and it satisfies robust property.
$$\mathsf {3POLY}\{p\}(X_1;\cdots ;X_{n}) \text { outputs } p(\mathbf {y}_1,\ldots ,\mathbf {y}_{N}), $$where \(X_1,\ldots ,X_{n}\) are partitions of \(\mathbf {y}_1,\ldots ,\mathbf {y}_N\).
-
Step III: We use \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}}\) to construct an \(n\)-party semi-honest MPC protocol \(\varPi _{\mathsf {sh}}^{F}\). This protocol is a four round protocol and it satisfies robust property.
We now describe the steps in detail.
Step I: Constructing \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) . Denote the parties by \(P_{1},P_{2}\) and \(P_{3}\). Denote the input of \(P_{1}\) to be \((x_1,r_1)\), the input of \(P_{2}\) to be \((x_2,r_2)\) and the input of \(P_{3}\) to be \((x_3)\). The protocol works as follows:
-
Round 1: \(P_{1}\) participates in a 1-out-of-2 oblivious transfer protocol \(\mathsf {OT}_{12}\) with \(P_{2}\). \(P_{1}\) plays the role of receiver. It generates the first message of \(\mathsf {OT}_{12}\) as a function of \(x_1\).
Simultaneously, \(P_{2}\) and \(P_{3}\) participate in a 1-out-of-2 protocol \(\mathsf {OT}_{23}\). \(P_{3}\) takes the role of the receiver. It generates the first message of \(\mathsf {OT}_{23}\) as a function of \(x_3\).
-
Round 2: \(P_{2}\) sends the second message in \(\mathsf {OT}_{12}\) as a function of \((x_2\cdot 0+r'_2;\ x_2\cdot 1+r'_2)\), where \(r'_2\) is sampled at random. \(P_{2}\) sends the second message in \(\mathsf {OT}_{23}\) as a function of \((0 \cdot r'_2+r_2;\ 1 \cdot r'_2+r_2)\).
Simultaneously, \(P_{1}\) and \(P_{3}\) participate in a \(\mathsf {OT}\) protocol \(\mathsf {OT}_{13}\). \(P_{3}\) takes the role of the receiver. It sends the first message of \(\mathsf {OT}_{13}\) as a function of \(x_3\).
-
Round 3: Let u be the value recovered by \(P_{1}\) from \(\mathsf {OT}_{12}\). \(P_{1}\) sends the second message to \(P_{3}\) in \(\mathsf {OT}_{13}\) as a function of \((u \cdot 0 + r_1,u \cdot 1 + r_1)\). Let \(\alpha '_{3}\) recovered from \(\mathsf {OT}_{13}\) by \(P_{3}\) and let \(\alpha ''_3\) be the output recovered from \(\mathsf {OT}_{23}\).
\(P_{1}\) outputs \(\alpha _1=r_1\), \(P_{2}\) outputs \(\alpha _2=r_2\) and \(P_{3}\) outputs \(\alpha _3=\alpha '_3+\alpha ''_3\) (operations performed over \(\mathbb {F}_2\)).
Theorem 6
Assuming the correctness of \(\mathsf {OT}\), \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) satisfies correctness property.
Theorem 7
Assuming the security of \(\mathsf {OT}\), \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) is a robust semi-honest three-party secure computation protocol satisfying Definition 5.
Step II: Constructing \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) . We first introduce some notation. Consider a polynomial \(q \in \mathbb {F}_2[{\mathbf {y}}_1,\ldots ,{\mathbf {y}}_{N}]\) with coefficients over \(\mathbb {F}_2\). We define the set \(\mathsf {MonS}\{q\}\) as follows: a term \(t \in \mathsf {MonS}\{q\}\) if and only if t appears in the expansion of the polynomial q. We define \(\mathsf {MonS}\{q\}_i\) as follows: a term \(t \in \mathsf {MonS}\{q\}_i\) if and only if \(t \in \mathsf {MonS}\{q\}\) and t contains the variable \(\mathbf {y}_i\).
We now describe \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\).
Protocol \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\): Let \(P_{1},\ldots ,P_{n}\) be the set of parties in the protocol. Let \(X_i\) be the input set of \(P_{i}\) for every \(i \in [n]\). We have, \(\sum _{i=1}^{n} |X_i|=N\) and \(X_i \cap X_j = \emptyset \) for \(i \ne j\). Every \(x \in X_i\) corresponds to a unique variable \(\mathbf {y}_j\) for some j.
-
For every \(i \in [n]\), party \(P_{i}\) generates \(n\) additive shares \(s_{i,1},\ldots ,s_{i,n}\) of 0. It sends share \(s_{i,j}\) to \(P_{j}\) in the first round.
-
In parallel, for every term t in the expansion of p, do the following:
-
- If t is of the form \(x_i^3\), then \(P_{i}\) computes \(x_i^3\).
-
- If t is of the form \(x_i^2 x_j\) then pick \(k \in [n]\) and \(k \ne i,k \ne j\). Let \(r_i^t\) and \(r_j^t\) be the randomness, associated with t, sampled by \(P_{i}\) and \(P_{j}\) respectively. The parties \(P_{i}(x_i,r_i^t),P_{j}(x_j,r_j^t)\) and \(P_{k}(1)\) execute \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) to obtain the corresponding shares \(\alpha _{i}^t,\alpha _{j}^t\) and \(\alpha _k^t\). Note that this finishes in the third round.
-
- If t is of the form \(x_ix_jx_k\), then parties \(P_{i},P_{j}\) and \(P_{k}\) sample randomness \(r_i^t,r_t^j\) and \(r^t_k\) respectively. Then, they execute \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) on inputs \((x_i,r_i^t)\), \((x_j,r_j^t)\) and \((x_k)\) to obtain the corresponding shares \(\alpha _{i}^t,\alpha _{j}^t\) and \(\alpha _k^t\). Note that this finishes in the third round.
-
-
After the third round, \(P_{i}\) adds all the shares he has so far (including his own shares) and he broadcasts his final share \(s_i\) to all the parties. This consumes one round.
-
Finally, \(P_{i}\) outputs \(\sum _{i=1}^{n} s_i\).
Theorem 8
Assuming \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) satisfies correctness, \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) satisfies correctness property.
Theorem 9
Assuming the security of \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\), \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) is a robust semi-honest MPC protcol satisfying Definition 5 as long as \(\varPi _{\mathsf {sh}}^{\mathsf {3MULT}}\) satisfies Definition 5.
Step III: Constructing \(\varPi _{\mathsf {sh}}^{F}\) . We describe \(\varPi _{\mathsf {sh}}^{F}\) below.
Protocol \(\varPi _{\mathsf {sh}}^{F}\): Let C be a circuit representing \(F\). That is, \(F(x_1;\ldots ,x_{n})=C(x_1||\cdots ||x_{n})\). Let \(\mathsf {RP}.\mathsf {CktE}(C)=(p_1,\ldots ,p_m)\). Note that \(p_i\), for every i, is a degree 3 polynomial in \(\mathbb {F}_2[\mathbf {y}_1,\ldots ,\mathbf {y}_{n}, \mathbf {r}_1,\ldots ,\mathbf {r}_N]\). Construct polynomial \(\hat{p_i} \in \mathbb {F}_2[\mathbf {y}_1,\ldots ,\mathbf {y}_{n},,\mathbf {r}_{1,1},\ldots ,\mathbf {r}_{n,N}]\) by replacing \(\mathbf {r}_j\), for every \(j \in [N]\), in \(p_i\) by the polynomial \(\sum _{k=1}^{n} \mathbf {r}_{k,j}\). Note that \(\hat{p_i}\) is still a degree 3 polynomial.
\(P_{i}\) samples randomness \(r_{i,j}\), for every \(j \in [N]\). For every \(j \in [m]\), all the parties execute the protocol \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{\hat{p_j}\}}\). The input of \(P_{i}\) is \((x_i,r_{i,1},\ldots ,r_{i,N})\) in this protocol. In the end, every party receives \(\alpha _j=\hat{p_j}(x_1,\ldots ,x_{n})\), for every \(j \in [m]\). Every party then executes \(\mathsf {D}(\alpha _1,\ldots ,\alpha _{n})\) to obtain \(\alpha ^*\). It outputs \(\alpha ^*\).
Theorem 10
Assuming the security of \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) and security of \(\mathsf {RP}\), \(\varPi _{\mathsf {sh}}^{F}\) is a robust semi-honest secure MPC protocol satisfying Definition 5 as long as \(\varPi _{\mathsf {sh}}^{\mathsf {3POLY}\{p\}}\) satisfies Definition 5.
The proofs can be found in the full version of the paper.
4 Five Round Malicious MPC
Overview. We start by giving an overview of our construction. We want to use the robust semi honest MPC as the basis for our construction, but its security is only defined in the semi-honest setting. We enforce the semi-honest setting by having the players prove, in parallel, that they computed the robust semi honest MPC honestly. Players prove that (1) they computed the first three rounds of the robust semi honest MPC honestly; and (2) they committed their input and randomness used in the robust semi honest MPC to every other party using both an extractable commitment scheme, and a non-interactive commitment scheme. To do so, we use a four round input delayed proof system, where the statement for the proof can be delayed till the final round. This lets players send the final round of their proof in the fourth round. Before proceeding, we verify each of the proofs received to ensure everyone is behaving in an honest manner. Next, to prove that the last round of the robust semi honest MPC is computed correctly, we use another instance of the four round input delayed proof system. The first three rounds run in parallel with the first three rounds of the protocol, but the last round of the proof system is delayed till the fifth round, after computing the last round of the robust semi honest MPC. This gives the total of five rounds.
Construction. For construction of the protocol, we require the following tools:
-
1.
A 3-round “rewinding-secure” extractable commitment scheme \(\varPi _\mathsf{rext}=\langle C_\mathsf{rext}, R_\mathsf{rext}\rangle \) (refer to definition in Sect. 2.5). We require the commitments to be well formed, where this property is defined in Sect. 2.5. Since there will be commitments in both directions for every pair of players, we introduce notation for individual messages of the protocol. \(\pi ^\mathrm {j}_{\mathsf{rext}_{\mathrm {k} \rightarrow \mathrm {i}}}\) refers to the \(\mathrm {j}\)-th round of the \(P_\mathrm {k}\)’s commitment to \(P_\mathrm {i}\).
We will denote by \(\tau _{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} := \left( \pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^2_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} \right) \).
-
2.
A non-interactive commitment scheme \(\varPi _\mathsf{nic}=\langle C_\mathsf{nic}, R_\mathsf{nic}\rangle \).
-
3.
A 4-round robust semi honest MPC protocol \(\varPi _\mathsf{rMPC}\) (refer to Definition 5) that has a next-message function \(\mathsf{nextMsg}^{\varPi _\mathsf{rMPC}}\) which, for player \(P_\mathrm {i}\), on input \((x_\mathrm {i}, r_\mathrm {i}, {\varvec{m}}^1,\cdots , {\varvec{m}}^\mathrm {j})\) returns \(m^{\mathrm {j}+1}_i\), the message \(P_\mathrm {i}\) broadcasts to all other players in the \((\mathrm {j}+1)\)-th round as a part of the protocol. Here \({\varvec{m}}^\mathrm {j}= (m^\mathrm {j}_1,\cdots ,m^\mathrm {j}_n)\) consists of all the messages sent during round \(\mathrm {j}\) of the protocol. The robust semi honest MPC also consists of a function \(\mathsf{Out}^{\varPi _\mathsf{rMPC}}\) that computes the final output y.
-
4.
Two 4-round delayed-input parallel non-malleable zero-knowledge protocols (refer to Definition 4). We use the variant of the NMZK protocol in [9] described earlier. (Our proof will make non-black box use of the NMZK.) \(\varPi _\mathsf{nmzk}=\langle P_\mathsf{nmzk}, V_\mathsf{nmzk}\rangle \) for the language
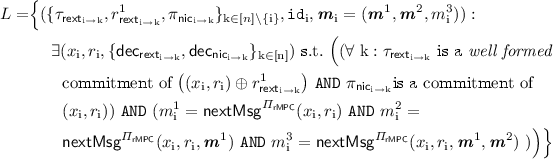
and \(\widehat{\varPi }_\mathsf{nmzk}=\langle \widehat{P}_\mathsf{nmzk}, \widehat{V}_\mathsf{nmzk}\rangle \) for the language
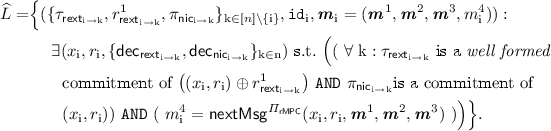
We represent by \(\pi ^\mathrm {j}_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) and \(\widehat{\pi }^\mathrm {j}_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) the messages sent in the \(\mathrm {j}\)-th round of \(P_\mathrm {k}\)’s proof to \(P_{\mathrm {i}}\) for an instance of L and \(\widehat{L}\) respectively.
Here L consists of instances where the player with identifier \(\mathtt{id}_\mathrm {i}\), \(P_{\mathrm {i}}\), correctly computes the first 3 rounds of the robust semi honest MPC with inputs \((x_i,r_i)\), and commits to this input to ever other player (in both commitments). Likewise, \(\widehat{L}\) consists of instances where the player with identifier \(\mathtt{id}_\mathrm {i}\), \(P_{\mathrm {i}}\), correctly computes the 4-th round of the robust semi honest MPC with inputs \((x_i,r_i)\), and commits to this input to ever other player (in both commitments).
Let \(\mathcal{P}= \lbrace P_1,\cdots ,P_\mathrm{n}\rbrace \) be the set of parties and \(\lbrace \mathtt{id}_1, \cdots , \mathtt{id}_\mathrm{n}\rbrace \) denote their corresponding unique identifiers (one can think of \(\mathtt{id}_\mathrm {i}=\mathrm {i}\)). The input and randomness \((x_i,r_i)\) to the robust semi honest MPC for player \(P_{\mathrm {i}}\) is fixed in the beginning of the protocol.
The protocol instructs each player \(P_{\mathrm {i}}\) to compute a message \(M^\mathrm {j}_\mathrm {i}\) for round \(\mathrm {j}\) and broadcasts it over the simultaneous broadcast channel. Thus in round \(\mathrm {j}\), messages \((M^\mathrm {j}_1,\cdots , M^\mathrm {j}_\mathrm{n})\) are simultaneously broadcast.
The protocol is detailed below. For ease of notation, we shall assume the that security parameter n is an implicit argument to each of the functions.
Round 1. Each player \(P_\mathrm {i}\) computes the message \(M^1_\mathrm {i}\) to be sent in the first round as follows:
-
1.
Compute independently, with fresh randomness, the first (committer) message of the “rewinding secure” extractable commitment for every other player. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$ r^0_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} \leftarrow \{0,1\}^{|(x_\mathrm {i},r_\mathrm {i})|};\,\, (\pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \mathsf{dec}_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} ) \leftarrow C_{\mathsf{rext}}(r^0_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}) $$Set \(\pi ^1_{\mathsf{rext}_\mathrm {i}} := ( \pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow 1}},\cdots ,\pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm{n}}})\).
-
2.
Compute independently, with fresh randomness, the non-interactive commitment for every other player. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$ (\pi _{\mathsf{nic}_{\mathrm {i} \rightarrow \mathrm {k}}}, \mathsf{dec}_{\mathsf{nic}_{\mathrm {i} \rightarrow \mathrm {k}}} ) \leftarrow C_{\mathsf{nic}}((x_\mathrm {i},r_\mathrm {i})) $$Set \(\pi _{\mathsf{nic}_\mathrm {i}} := ( \pi _{\mathsf{nic}_{\mathrm {i} \rightarrow 1}},\cdots ,\pi _{\mathsf{nic}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\pi _{\mathsf{nic}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \pi _{\mathsf{nic}_{\mathrm {i} \rightarrow \mathrm{n}}})\).
-
3.
Compute independently, with fresh randomness, the first (verifier) message of both non-malleable zero-knowledge protocols for every other player. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$\begin{aligned} \pi ^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}} \leftarrow V_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {k},\ell ),\,\, \widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}} \leftarrow \widehat{V}_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {k},\widehat{\ell }) \end{aligned}$$where \(\ell \) and \(\widehat{\ell }\) are the lengths of the input delayed statements for L and \(\widehat{L}\) respectively.
Set
$$\begin{aligned} \pi ^1_{\mathsf{nmzk}_\mathrm {i}}&:= ( \pi ^1_{\mathsf{nmzk}_{1 \rightarrow \mathrm {i}}},\cdots ,\pi ^1_{\mathsf{nmzk}_{\mathrm {i}-1 \rightarrow \mathrm {i}}},\perp ,\pi ^1_{\mathsf{nmzk}_{\mathrm {i}+1 \rightarrow \mathrm {i}}},\cdots , \pi ^1_{\mathsf{nmzk}_{\mathrm{n} \rightarrow \mathrm {i}}})\\ \widehat{\pi }^1_{\mathsf{nmzk}_\mathrm {i}}&:= ( \widehat{\pi }^1_{\mathsf{nmzk}_{1 \rightarrow \mathrm {i}}},\cdots ,\widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {i}-1 \rightarrow \mathrm {i}}},\perp ,\widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {i}+1 \rightarrow \mathrm {i}}},\cdots , \widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm{n} \rightarrow \mathrm {i}}})\\ \end{aligned}$$
\(M^1_\mathrm {i}\) is now defined as, \(M^1_\mathrm {i}:= (\pi ^1_{\mathsf{rext}_\mathrm {i}}, \pi _{\mathsf{nic}_\mathrm {i}}, \pi ^1_{\mathsf{nmzk}_\mathrm {i}}, \widehat{\pi }^1_{\mathsf{nmzk}_\mathrm {i}})\). Broadcast \(M^1_\mathrm {i}\) and receive \(M^1_1, \cdots , M^1_{\mathrm {i}-1}, M^1_{\mathrm {i}+1}, \cdots , M^1_\mathrm{n}\).
Round 2. Each player \(P_\mathrm {i}\) computes the message \(M^2_\mathrm {i}\) to be sent in the second round as follows:
-
1.
Compute the second message of the “rewinding secure” extractable commitment in response to the messages from the other parties. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$ \pi ^2_{\mathsf{rext}_{\mathrm {k} \rightarrow \mathrm {i}}} \leftarrow R_{\mathsf{rext}}(\pi ^1_{\mathsf{rext}_{\mathrm {k} \rightarrow \mathrm {i}}}) $$where \(\pi ^1_{\mathsf{rext}_{\mathrm {k} \rightarrow \mathrm {i}}}\) can be obtained from \(\pi ^1_{\mathsf{rext}_\mathrm {k}}\) in \(M^1_\mathrm {k}\).
Set \(\pi ^2_{\mathsf{rext}_\mathrm {i}} := ( \pi ^2_{\mathsf{rext}_{1 \rightarrow \mathrm {i}}},\cdots ,\pi ^2_{\mathsf{rext}_{\mathrm {i}-1 \rightarrow \mathrm {i}}},\perp ,\pi ^2_{\mathsf{rext}_{\mathrm {i}+1 \rightarrow \mathrm {i}}},\cdots , \pi ^2_{\mathsf{rext}_{\mathrm{n} \rightarrow \mathrm {i}}})\).
-
2.
Compute the second message of both non-malleable zero-knowledge protocols in response to the messages from the other parties. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$\begin{aligned} \pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}} \leftarrow P_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {i},\ell , \pi ^1_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}});\,\, \widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}} \leftarrow \widehat{P}_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {i},\widehat{\ell }, \widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}) \end{aligned}$$where \(\pi ^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) and \(\widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) can be obtained from \(\pi ^1_{\mathsf{nmzk}_\mathrm {k}}\) and \(\widehat{\pi }^1_{\mathsf{nmzk}_\mathrm {k}}\) respectively in \(M^1_\mathrm {k}\). Set
$$\begin{aligned} \pi ^2_{\mathsf{nmzk}_\mathrm {i}}&:= ( \pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow 1}},\cdots ,\pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm{n}}})\\ \widehat{\pi }^2_{\mathsf{nmzk}_\mathrm {i}}&:= ( \widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow 1}},\cdots ,\widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm{n}}}) \end{aligned}$$ -
3.
Compute the first message of the robust semi honest MPC,
$$ m^{1}_{\mathrm {i}} \leftarrow \mathsf{nextMsg}^{\varPi _\mathsf{rMPC}}(x_\mathrm {i}, r_\mathrm {i}). $$
\(M^2_\mathrm {i}\) is now defined as, \(M^2_\mathrm {i}:= (\pi ^2_{\mathsf{rext}_\mathrm {i}}, \pi ^2_{\mathsf{nmzk}_\mathrm {i}}, \widehat{\pi }^2_{\mathsf{nmzk}_\mathrm {i}}, m^1_\mathrm {i})\). Broadcast \(M^2_\mathrm {i}\) and receive \(M^2_1, \cdots , M^2_{\mathrm {i}-1}, M^2_{\mathrm {i}+1}, \cdots , M^2_\mathrm{n}\).
Round 3. Each player \(P_\mathrm {i}\) computes the message \(M^3_\mathrm {i}\) to be sent in the third round as follows:
-
1.
Compute the final message of the “rewinding secure” extractable commitment. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$ \pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} \leftarrow C_{\mathsf{rext}}( \pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^2_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}) $$where \(\pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is as computed earlier and \(\pi ^2_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is obtained from \(\pi ^2_{\mathsf{rext}_\mathrm {k}}\) in \(M^2_\mathrm {k}\). Set \(\pi ^3_{\mathsf{rext}_\mathrm {i}} := ( \pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow 1}},\cdots ,\pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm{n}}})\).
-
2.
Compute \((x_\mathrm {i},r_\mathrm {i})\) masked with the randomness sent in the “rewinding secure” extractable commitment, i.e. \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$ r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} := r^0_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} \oplus (x_\mathrm {i},r_\mathrm {i}) $$Set \(r^1_{\mathsf{rext}_\mathrm {i}} := ( r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow 1}},\cdots ,r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm{n}}}).\)
-
3.
Compute the third message of both non-malleable zero-knowledge protocols. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
$$\begin{aligned} \pi ^3_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}&\leftarrow V_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {k}, \pi ^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}, \pi ^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}) \\ \widehat{\pi }^3_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}&\leftarrow \widehat{V}_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {k}, \widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}, \widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}) \end{aligned}$$where \(\pi ^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) is as computed earlier and \(\pi ^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) is obtained from \(\pi ^2_{\mathsf{nmzk}_\mathrm {k}}\) in \(M^2_\mathrm {k}\). \(\widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) and \(\widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) are obtained similarly.
Set
$$\begin{aligned} \pi ^3_{\mathsf{nmzk}_\mathrm {i}}&:= ( \pi ^3_{\mathsf{nmzk}_{1 \rightarrow \mathrm {i}}},\cdots ,\pi ^3_{\mathsf{nmzk}_{\mathrm {i}-1 \rightarrow \mathrm {i}}},\perp ,\pi ^3_{\mathsf{nmzk}_{\mathrm {i}+1 \rightarrow \mathrm {i}}},\cdots , \pi ^3_{\mathsf{nmzk}_{\mathrm{n} \rightarrow \mathrm {i}}})\\ \widehat{\pi }^3_{\mathsf{nmzk}_\mathrm {i}}&:= ( \widehat{\pi }^3_{\mathsf{nmzk}_{1 \rightarrow \mathrm {i}}},\cdots ,\widehat{\pi }^3_{\mathsf{nmzk}_{\mathrm {i}-1 \rightarrow \mathrm {i}}},\perp ,\widehat{\pi }^3_{\mathsf{nmzk}_{\mathrm {i}+1 \rightarrow \mathrm {i}}},\cdots , \widehat{\pi }^3_{\mathsf{nmzk}_{\mathrm{n} \rightarrow \mathrm {i}}}) \end{aligned}$$ -
4.
Compute the second message of the robust semi honest MPC,
$$ m^{2}_{\mathrm {i}} \leftarrow \mathsf{nextMsg}^{\varPi _\mathsf{rMPC}}(x_\mathrm {i}, r_\mathrm {i}, {\varvec{m}}^1) $$where \({\varvec{m}}^1 := (m^1_1,\cdots ,m^1_\mathrm{n})\).
\(M^3_\mathrm {i}\) is now defined as, \(M^3_\mathrm {i}:= (\pi ^3_{\mathsf{rext}_\mathrm {i}},r^1_{\mathsf{rext}_\mathrm {i}}, \pi ^3_{\mathsf{nmzk}_\mathrm {i}}, \widehat{\pi }^3_{\mathsf{nmzk}_\mathrm {i}}, m^2_\mathrm {i})\). Broadcast \(M^3_\mathrm {i}\) and receive \(M^3_1, \cdots , M^3_{\mathrm {i}-1}, M^3_{\mathrm {i}+1}, \cdots , M^3_\mathrm{n}\).
Round 4. Each player \(P_\mathrm {i}\) computes the message \(M^4_\mathrm {i}\) to be sent in the fourth round as follows:
-
1.
Compute the third message of the robust semi honest MPC,
$$ m^{3}_{\mathrm {i}} \leftarrow \mathsf{nextMsg}^{\varPi _\mathsf{rMPC}}(x_\mathrm {i}, r_\mathrm {i}, {\varvec{m}}^1, {\varvec{m}}^2) $$where \({\varvec{m}}^1 := (m^1_1,\cdots ,m^1_\mathrm{n})\) and \({\varvec{m}}^2 := (m^2_1,\cdots ,m^2_\mathrm{n})\).
-
2.
Compute the final message of the non-malleable zero-knowledge protocol for language L. i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
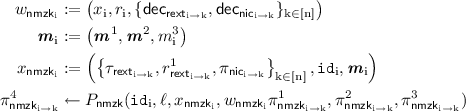
where \(|x_{\mathsf{nmzk}_\mathrm {i}}| = \ell \), and \(\pi ^1_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is obtained from \(\pi ^1_{\mathsf{nmzk}_\mathrm {k}}\) in \(M^1_\mathrm {k}\). Similarly, \(\pi ^3_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is be obtained from \(\pi ^3_{\mathsf{nmzk}_\mathrm {k}}\) in \(M^3_\mathrm {k}\). \(\pi ^2_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is as computed earlier.
Set \(\pi ^4_{\mathsf{nmzk}_\mathrm {i}} := ( \pi ^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow 1}},\cdots ,\pi ^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\pi ^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \pi ^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm{n}}})\).
\(M^4_\mathrm {i}\) is now defined as, \(M^4_\mathrm {i}:= (\pi ^4_{\mathsf{nmzk}_\mathrm {i}}, m^3_\mathrm {i})\). Broadcast \(M^4_\mathrm {i}\) and receive \(M^4_1, \cdots , M^4_{\mathrm {i}-1}, M^4_{\mathrm {i}+1}, \cdots , M^4_\mathrm{n}\).
Round 5. Each player \(P_\mathrm {i}\) computes the message \(M^5_\mathrm {i}\) to be sent in the fifth round as follows:
-
1.
Check if all the proofs in the protocol are accepting. The proof from \(P_\mathrm {k}\) to \(P_{\mathrm {j}}\) is accepting if \(P_\mathrm {k}\) has computed the first 3 rounds of the robust semi honest MPC correctly and has committed to the same inputs, used in the robust semi honest MPC, to every other player. First, compute the statement \(x_{\mathsf{nmzk}_\mathrm {k}}\) for each player \(P_\mathrm {k}\). i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
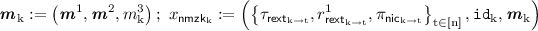
Next, check if every proof is valid.
$$\begin{aligned} \text {if } \exists \mathrm {k}, \mathrm {j}\text { s.t } \mathsf{accept}&\ne V_{\mathsf{nmzk}}(\mathtt{id}_\mathrm {k}, x_{\mathsf{nmzk}_\mathrm {k}}, \pi ^1_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {j}}}, \pi ^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {j}}}, \pi ^3_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {j}}}, \pi ^4_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {j}}})\\&\text { then } \mathsf{output \perp \text { and } abort}\\ \text {else continue}&\end{aligned}$$This can be done because the proofs are public coin. Moreover this is done to avoid the case that some honest parties continue on to the next round, but the others abort.
-
2.
Compute the final message of the robust semi honest MPC,
$$ m^{4}_{\mathrm {i}} \leftarrow \mathsf{nextMsg}^{\varPi _\mathsf{rMPC}}(x_\mathrm {i}, r_\mathrm {i}, {\varvec{m}}^1, {\varvec{m}}^2, {\varvec{m}}^3) $$where \({\varvec{m}}^1 := (m^1_1,\cdots ,m^1_\mathrm{n})\), \({\varvec{m}}^2 := (m^2_1,\cdots ,m^2_\mathrm{n})\) and \({\varvec{m}}^3 := (m^3_1,\cdots ,m^3_\mathrm{n})\).
-
3.
Compute the final message of the non-malleable zero-knowledge protocol for language \(\widehat{L}\). i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
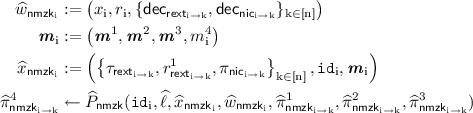
where \(|\widehat{x}_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}| = \widehat{\ell }\), and \(\widehat{\pi }^1_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is obtained from \(\widehat{\pi }^1_{\mathsf{nmzk}_\mathrm {k}}\) in \(M^1_\mathrm {k}\). Similarly, \(\widehat{\pi }^3_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {k}}}\) is obtained from \(\widehat{\pi }^3_{\mathsf{nmzk}_\mathrm {k}}\) in \(M^3_\mathrm {k}\). \(\widehat{\pi }^2_{\mathsf{nmzk}_{\mathrm {k} \rightarrow \mathrm {i}}}\) is as computed earlier. Set \(\widehat{\pi }^4_{\mathsf{nmzk}_\mathrm {i}} := ( \widehat{\pi }^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow 1}},\cdots ,\widehat{\pi }^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}-1}},\perp ,\widehat{\pi }^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm {i}+1}},\cdots , \widehat{\pi }^4_{\mathsf{nmzk}_{\mathrm {i} \rightarrow \mathrm{n}}})\)
\(M^5_\mathrm {i}\) is now defined as, \(M^5_\mathrm {i}:= (m^4_\mathrm {i}, \widehat{\pi }^4_{\mathsf{nmzk}_\mathrm {i}})\). Broadcast \(M^5_\mathrm {i}\) and receive \(M^5_1, \cdots , M^5_{\mathrm {i}-1}, M^5_{\mathrm {i}+1}, \cdots , M^5_\mathrm{n}\).
Output Computation. To compute the output, \(P_{\mathrm {i}}\) performs the following steps:
-
1.
Check if all the proofs in the protocol are accepting. The proof from \(P_\mathrm {k}\) to \(P_\mathrm {j}\) is accepting if \(P_\mathrm {k}\) has computed the 4-th round of the robust semi honest MPC correctly and has committed to the same inputs, used in the robust semi honest MPC, to every other party.
First, compute the statement \(\widehat{x}_{\mathsf{nmzk}_\mathrm {k}}\) for each player \(P_\mathrm {k}\). i.e., \(\forall \mathrm {k}\in [\mathrm{n}]\setminus \lbrace \mathrm {i}\rbrace \)
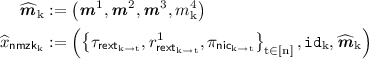
Next, check if every proof is valid.
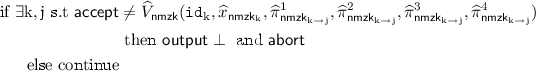
-
2.
Compute the output of the protocol as
$$ y \leftarrow \mathsf{Out}^{\varPi _\mathsf{rMPC}}(x_\mathrm {i},r_\mathrm {i},{\varvec{m}}^1,{\varvec{m}}^2,{\varvec{m}}^3, {\varvec{m}}^4) $$
Theorem 11
Assuming security of the “rewinding secure” extractable commitment, non-interactive commitment scheme, robust semi-honest MPC and NMZK, the above described five round protocol is secure against malicious adversaries.
We use the standard definition of security with abort against malicious adversaries (see [15] for details).
Extractable commitments and NMZK can be instantiated from DL, while the robust semi-honest MPC can be instantiated from DDH. Thus, all the required primitives can be instantiated from DDH.
The complete proof can be found in the full version of our paper, but we give an overview of the simulator below. Before we proceed to the simulator, we discuss a few properties of the underlying primitives that we will need:
-
Recall that simulator for the robust semi honest MPC consists of two parts. The first part, \(\mathsf{Sim}^1_\mathsf{rMPC}\), simulates the first three rounds of the robust semi honest MPC without requiring inputs or outputs of the adversary. The second part, \(\mathsf{Sim}^2_\mathsf{rMPC}\), when given the inputs, random tape and outputs a simulated transcript of the last round that is consistent with the input and randomness. Additionally, note that this simulation succeeds as long as the adversary behaved honestly in the first three rounds of the robust semi honest MPC.
-
The extractor for the 3 round “rewinding secure” extractable commitment works by rewinding the second and third round polynomial number of times. From Lemma 1, we know that if the commitments are well formed, extraction fails with only negligible probability.
-
The simulator of the NMZKs works by extracting a trapdoor. Specifically, it rewinds the second and third round polynomial number of times to get signatures for two distinct messages. Further, this extraction fails only with negligible probability.
-
Combining the above two properties, we see that the rewindings of NMZK and the “rewinding secure” extractable commitment are “composable” because they rewind in the same rounds in our MPC protocol.
We describe the ideal world simulator \(\mathsf{Sim}\) below. We shall denote the set of honest players by \(\mathcal{H}\) and the set of corrupted players by \(\mathcal{P}^\mathcal {A}\).
-
1.
The first three rounds of protocol are simulated as follows:
-
For the robust semi honest MPC, since \({\mathsf{Sim}}^1_\mathsf{rMPC}\) doesn’t require any input or output to simulate the first three rounds, we use it directly to obtain \(\left\{ m^1_\mathrm {i}, m^2_\mathrm {i}, m^3_\mathrm {i}\right\} _{P_{\mathrm {i}} \in \mathcal{H}}\). Since the robust semi honest MPC starts from the second round, \(\left\{ m^3_\mathrm {i}\right\} _{P_{\mathrm {i}} \in \mathcal{H}}\) is sent in the 4th round with the last round of the NMZK for L, but we group them here for simplicity.
-
For simulating proofs for the NMZKs, we deal with three different cases:
-
(a)
For proofs from the adversary, the honest player acts as a verifier. In this case, fix a random tape for the verifier and respond honestly to adversary queries.
-
(b)
For proofs within honest players, we fix the random tape for the verifiers and thus can trivially compute the trapdoor in the NMZKs for both languages using the verifier’s random tape.
-
(c)
For proofs from honest players to the adversary, we run the simulators \(\mathsf{Sim}_\mathsf{nmzk}\) and \(\widehat{\mathsf{Sim}}_\mathsf{nmzk}\) to simulate the first three rounds. This internally rewinds polynomial many times to obtain the trapdoors. If the extractor fails, output \(\bot _\mathsf{nmzk}\) and abort.
-
(a)
-
For the “rewinding secure” extractable commitment, we deal with two cases:
-
(a)
For commitments from the honest players to the adversary, we just commit to the all ‘0’ string. We do this for commitments within the honest players as well.
-
(b)
For commitments where the honest players are recipients, run the extractor to send responses and extract the values inside the commitments. If extractor fails, output \(\bot _\mathsf{rext}\) and abort.
-
(a)
-
For the non-interactive commitments, commit to the all ‘0’ string for commitments from the honest players to the adversary.
-
For the masked value in the third round, send the same random string as committed earlier in the “rewinding secure” extractable commitment.
As noted earlier, the rewinding performed within the NMZK simulator and the extractor for “rewinding secure” extractable commitments work in the same rounds and can be performed for each without affecting the other. Additionally, these extracted values along with the masked values sent by the adversary gives us its input and randomness.
-
-
2.
Simulate the last round of the NMZK for L in two steps.
-
For proofs from the honest parties to the adversary, use \({\mathsf{Sim}}_\mathsf{nmzk}\) and the trapdoors obtained to compute the last round of the NMZK for L.
-
For proofs within honest parties, the trapdoor is trivially known to the simulator and thus compute the last round of the NMZK for L.
On receiving the proofs for L from the adversary, check if all the received proofs are valid. This is equivalent to checking if all proofs in the protocol verify. If the check fails, send abort to the ideal functionality and exit.
-
-
3.
We perform an additional check before we obtain the final round of the robust semi honest MPC. Given \({\varvec{m}}^1, {\varvec{m}}^2, {\varvec{m}}^3, \left\{ (x_k,r_k)\right\} _{P_{\mathrm {k}} \in \mathcal{P}^\mathcal {A}}\), we check if the adversary has followed the computation in the first three rounds correctly. If the check fails we output \(\bot ^1_\mathsf{rMPC}\) and abort. It is implicit that the proofs for L have verified prior to this step.
-
4.
Send the extracted inputs \(\lbrace x_k\rbrace _{P_{\mathrm {k}} \in \mathcal{P}^\mathcal {A}}\) to the ideal functionality to obtain the output y.
Compute the final round (of all players) of the robust semi honest MPC as
$$ \left\{ m^4_\mathrm {i}\right\} _{P_{\mathrm {i}} \in \mathcal{P}} \leftarrow \mathsf{Sim}^2_\mathsf{rMPC}\left( {\varvec{m}}^1, {\varvec{m}}^2, {\varvec{m}}^3, \lbrace x_\mathrm {k}\rbrace _{P_{\mathrm {k}} \in \mathcal{P}^\mathcal {A}}, \lbrace r_\mathrm {k}\rbrace _{P_{\mathrm {k}} \in \mathcal{P}^\mathcal {A}}, y \right) . $$Additionally, simulate the last round of the NMZK for \(\widehat{L}\). This is done in two steps
-
For proofs from the honest parties to the adversary, use \(\widehat{\mathsf{Sim}}_\mathsf{nmzk}\) and the trapdoors obtained to compute the last round of the NMZK for \(\widehat{L}\).
-
For proofs within honest parties, the trapdoor is trivially known to the adversary and thus compute the last round of the NMZK for \(\widehat{L}\).
-
-
5.
On receiving the proofs for \(\widehat{L}\) from the adversary check if all the received proofs are valid. If the check fails, send abort to the ideal functionality.
Otherwise, on receiving \(\left\{ m^{*4}_\mathrm {k}\right\} _{ P_\mathrm {k}\in \mathcal{P}^\mathcal {A}}\) from the adversary, we check if it matches the transcript simulated by \(\mathsf{Sim}^2_\mathsf{rMPC}\) earlier. If not, but the proofs above have verified output \(\bot ^2_\mathsf{rMPC}\) and abort. Else send continue to the ideal functionality.
5 Four Round Malicious MPC
Overview. We give an overview of our four round construction. At a high-level, the four round protocol is very similar to the five round protocol (from the previous section) but to compress the number of rounds we cannot have two instances of the four-round NMZK as before. Instead, we use a 3 round input-delayed strong WI argument of knowledge (with appropriate non-malleability properties), ending in the third round, to enable parties to prove their honest behavior of the first three rounds. This lets the players send the fourth message in the clear if the proof at the end of the third round verifies. For the output round, we use a four-round NMZK as before to prove honest behavior.
The three-round input-delayed proof system that we use to establish honest behavior in the first three rounds is depicted in Fig. 1. We do not argue its security separately, but within the hybrids of our overall security proof. We present the construction with 2-round non-malleable commitment for simplicity, but a 3-round non-malleable commitment can also be used. The required complexity leveraging levels for the proof are different in each case.
Proof for a language L using this proof system requires:
-
Prover committing to 0 using a 2-round non-malleable commitment [28]. The relevance of this will become clear shortly.
-
The verifier sends the image of the one way permutation applied on a random string r.
-
An input delayed witness indistinguishable proof of knowledge (WIPoK) proving knowledge of either: (1) w such that \((x,w) \in \mathsf{Rel}_L\) and the non-malleable commitment decommits to 0; or (2) the decommitment of the non-malleable commitment to pre-image r of the one way permutation. Informally speaking, one can think of the above construction as a strong input delayed WI argument of knowledge with non-malleability properties.
Construction. For construction of the protocol, we require the tools described below. The exact security levels for each of these primitives are discussed at the end of the construction.
-
1.
A one-way permutation f.
-
2.
A 3-round “rewinding secure” extractable commitment scheme \(\varPi _\mathsf{rext}=\langle C_\mathsf{rext}, R_\mathsf{rext}\rangle \) (refer to definition in Sect. 2.5).
-
3.
A non-interactive commitment scheme \(\varPi _\mathsf{nic}=\langle C_\mathsf{nic}, R_\mathsf{nic}\rangle \).
-
4.
An instance of a 2-round (private coin) extractable non-malleable commitment scheme \({\varPi }_\mathsf{nmcom}=\langle C_\mathsf{nmcom}, R_\mathsf{nmcom}\rangle \). These can be constructed from the assumption of sub-exponentially hard DDH [28].Footnote 10
We will use the following notation throughout the protocol for the various commitment schemes
$$\begin{aligned} \tau _{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} := \left( \pi ^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^2_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^3_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}} \right) ;~ \tau _{\mathsf{nmcom}_{\mathrm {i} \rightarrow \mathrm {k}}} := \left( \pi ^1_{\mathsf{nmcom}_{\mathrm {i} \rightarrow \mathrm {k}}}, \pi ^2_{\mathsf{nmcom}_{\mathrm {i} \rightarrow \mathrm {k}}} \right) \end{aligned}$$ -
5.
A 4-round robust semi-honest MPC protocol \(\varPi _\mathsf{rMPC}\) as described in the five round protocol.
-
6.
A 3 round input delayed witness indistinguishable proof of knowledge (WIPoK) protocol \(\varPi _\mathsf{WIPoK}=(P_\mathsf{WIPoK}, V_\mathsf{WIPoK})\) for the language \(L_\mathsf{WIPoK}\). We require the protocols to be public coin and instantiate them using the Lapidot-Shamir protocol [29]. For the sake of readability and clarity, we modularize the language to obtain the final language.

L is the language which consists of instances where player \(P_{\mathrm {i}}\) correctly computes the first three rounds of the robust semi honest MPC with inputs \((x_\mathrm {i}, r_\mathrm {i})\), commits to \((x_\mathrm {i}, r_\mathrm {i}) \oplus r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}\) to every other player \(P_\mathrm {k}\) in the “rewinding secure” extractable commitment and commits to \((x_\mathrm {i}, r_\mathrm {i})\) to every other player \(P_\mathrm {k}\) in the non-interactive commitment. Additionally, we require that the commitments in each of these “rewinding secure” extractable commitment is well formed. We define
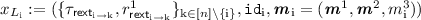 .
. 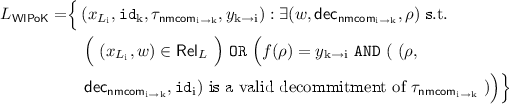
\(L_\mathsf{WIPoK}\) consists of instances where player \(P_{\mathrm {i}}\) proves to player \(P_{\mathrm {k}}\) that either
-
it behaved honestly, i.e. it has a witness w such that \((x_{L_\mathrm {i}},w)\in \mathsf{Rel}_L\); or
-
it possesses the trapdoor mentioned earlier, and has committed to it in the non-malleable commitment.
We define \(x_{{\mathsf{WIPoK}_{\mathrm {i} \rightarrow \mathrm {k}}}}:= \left( x_{L_\mathrm {i}}, \mathtt{id}_\mathrm {k}, \tau _{\mathsf{nmcom}_{\mathrm {i} \rightarrow \mathrm {k}}} , y_{\mathrm {k} \rightarrow \mathrm {i}} \right) \).
-
-
7.
A 4-round delayed-input parallel non-malleable zero-knowledge protocols (refer to Definition 4). We use a variant the NMZK protocol in [9] described earlier. Our proof will make non-black box use of the NMZK. \(\varPi _\mathsf{nmzk}=\langle P_\mathsf{nmzk}, V_\mathsf{nmzk}\rangle \) for the language
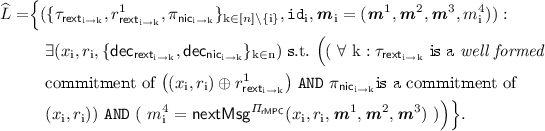
\(\widehat{L}\) is the language which consists of instances where player \(P_{\mathrm {i}}\) (a) correctly computed the final round of the robust MPC with inputs \((x_\mathrm {i}, r_\mathrm {i})\); (b) commits to \((x_\mathrm {i}, r_\mathrm {i}) \oplus r^1_{\mathsf{rext}_{\mathrm {i} \rightarrow \mathrm {k}}}\) to every other player \(P_\mathrm {k}\) in the “rewinding secure” extractable commitment such that they are well formed; and (c) commits to \((x_\mathrm {i}, r_\mathrm {i})\) to every other player \(P_\mathrm {k}\) in the non-interactive commitment. We define
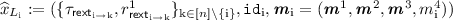 .
.
We briefly describe each round of the protocol. A complete description of the protocol can be found in the full version.
Round 1. Each player \(P_\mathrm {i}\) computes the message \(M^1_\mathrm {i}\) to be broadcast in the first round constituting of:
-
1.
The first (committer) message of the “rewinding secure” extractable commitment for every other player, computed independently with fresh randomness.
-
2.
Commit to the input and randomness to every other player independently with fresh randomness, using the non-interactive commitment.
-
3.
The first message of the robust semi honest MPC.
-
4.
The different components that make up the proof system for L, computed independently for every other player. This includes the image of the one-way permutation on a random string, the first (receiver) message of the non-malleable commitment and the first message for the input delayed witness indistinguishable proof of knowledge (WIPoK) for \(L_\mathsf{WIPoK}\).
-
5.
The first (verifier) message of the non-malleable zero-knowledge protocol for every other player, computed independently with fresh randomness.
Round 2. Each player \(P_\mathrm {i}\) computes the message \(M^2_\mathrm {i}\) to be broadcast in the second round consisting of:
-
1.
The second message of the “rewinding secure” extractable commitment in response to the messages from the other parties.
-
2.
The second message of the robust semi honest MPC,
-
3.
The second message for the different components in the proof system for L. This includes the second message of the non-malleable commitment scheme and the second message of the input delayed WIPoK for \(L_\mathsf{WIPoK}\), in response to messages from every other player.
-
4.
The second message of the non-malleable zero-knowledge protocols in response to the messages from the other parties.
Round 3. Each player \(P_\mathrm {i}\) computes the message \(M^3_\mathrm {i}\) to be broadcast in the third round constituting of:
-
1.
The final message of the “rewinding secure” extractable commitment.
-
2.
\((x_\mathrm {i},r_\mathrm {i})\) masked with the randomness sent in the “rewinding secure” extractable commitment. Here \((x_\mathrm {i},r_\mathrm {i})\) is the input and randomness used by \(P_{\mathrm {i}}\) in the robust semi honest MPC.
-
3.
The third message of the robust semi honest MPC.
-
4.
The final message WIPoK for language \(L_\mathsf{WIPoK}\).
-
5.
The third message of the non-malleable zero-knowledge protocol.
Round 4. Each player \(P_\mathrm {i}\) computes the message \(M^4_\mathrm {i}\) to be broadcast in the fourth round:
-
1.
The final message of the robust semi honest MPC. Prior to computing the final message, \(P_{\mathrm {i}}\) checks if proofs for \(L_\mathsf{WIPoK}\) between every pair of players are accepting. This is possible since the proofs are public coin and have been previously broadcast. If the proofs fail, \(P_{\mathrm {i}}\) aborts the protocol.
-
2.
The final message of the non-malleable zero-knowledge protocol for language \(\widehat{L}\).
Output Computation. To compute the output, \(P_{\mathrm {i}}\) performs the following steps:
-
1.
Check if proofs between every pair of players for \(\widehat{L}_\mathsf{WIPoK}\) are accepting. As before, abort if the check fails.
-
2.
Compute the output of the protocol.
In the full version of our paper [1], we prove the security of the above protocol where we rely on complexity leveraging between various primitives. Overall, our construction can be based on one-way permutation and sub-exponential DDH.
Notes
- 1.
Garg et al. also construct a four-round protocol for the coin-tossing functionality. In this work, we are interested in MPC for general functions.
- 2.
We use low-depth PRGs to obtain degree-three randomizing polynomials for general functions [2].
- 3.
- 4.
Note that the witness for these proofs corresponds to the adversary’s input and random tape which is already fixed in the first round.
- 5.
We also use the fact that argument system of [9] allows for simulating multiple proofs executed in parallel.
- 6.
We believe that some of the use of complexity leveraging in our hybrids can be avoided by modifications to our protocol. We leave further exploration of this direction for subsequent work.
- 7.
A randomized encoding of function f and input x is such that, the output f(x) can be recovered from this encoding and at the same time, this encoding should not leak any information about either f or x.
- 8.
The terms randomized encodings and randomizing polynomials are interchangeably used.
- 9.
It actually proves that the non-malleable commitment contains the masked witness, where the mask is sent separately. But we ignore this technicality for the discussion.
- 10.
While in all other cases, we have required the use of public coins, we can make do with a private coin protocol here. This will become apparent in the proof.
References
Ananth, P., Choudhuri, A.R., Jain, A.: A new approach to round-optimal secure multiparty computation. IACR Cryptology ePrint Archive 2017, 402 (2017). http://eprint.iacr.org/2017/402
Applebaum, B., Ishai, Y., Kushilevitz, E.: Computationally private randomizing polynomials and their applications. Comput. Complex. 15(2), 115–162 (2006)
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_29
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Barak, B., Prabhakaran, M., Sahai, A.: Concurrent non-malleable zero knowledge. In: 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2006), Berkeley, California, USA, Proceedings, 21–24 October 2006, pp. 345–354 (2006)
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, Baltimore, Maryland, USA, 13–17 May 1990, pp. 503–513 (1990)
Brakerski, Z., Halevi, S., Polychroniadou, A.: Four round secure computation without setup. IACR Cryptology ePrint Archive 2017, 386 (2017). http://eprint.iacr.org/2017/386
Chandran, N., Goyal, V., Ostrovsky, R., Sahai, A.: Covert multi-party computation. In: 48th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2007, pp. 238–248. IEEE (2007)
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: 4-round concurrent non-malleable commitments from one-way functions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10401, pp. 127–157. Springer, Cham (2017)
Even, S., Goldreich, O., Lempel, A.: A randomized protocol for signing contracts. In: Advances in Cryptology: Proceedings of CRYPTO 1982, Santa Barbara, California, USA, 23–25 August 1982, pp. 205–210 (1982)
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_4
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS, pp. 40–49 (2013)
Garg, S., Goyal, V., Jain, A., Sahai, A.: Concurrently secure computation in constant rounds. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 99–116. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_8
Garg, S., Mukherjee, P., Pandey, O., Polychroniadou, A.: The exact round complexity of secure computation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 448–476. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_16
Goldreich, O.: Foundations of Cryptography: Volume 2, Basic Applications, vol. 2. Cambridge University Press, Cambridge (2009)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game. In: STOC (1987)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems. In: STOC, pp. 291–304 (1985)
Goyal, V.: Constant round non-malleable protocols using one way functions. In: Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC 2011, San Jose, CA, USA, 6–8 June 2011, pp. 695–704 (2011)
Goyal, V.: Positive results for concurrently secure computation in the plain model. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS 2012, New Brunswick, NJ, USA, 20–23 October 2012, pp. 41–50 (2012)
Goyal, V., Jain, A.: On the round complexity of covert computation. In: Proceedings of the Forty-Second ACM Symposium on Theory of Computing, pp. 191–200. ACM (2010)
Goyal, V., Jain, A., Ostrovsky, R.: Password-authenticated session-key generation on the internet in the plain model. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 277–294. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_15
Goyal, V., Pandey, O., Richelson, S.: Textbook non-malleable commitments. In: STOC, pp. 1128–1141 (2016)
Goyal, V., Richelson, S., Rosen, A., Vald, M.: An algebraic approach to non-malleability. In: FOCS, pp. 41–50 (2014)
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st Annual Symposium on Foundations of Computer Science, 2000, Proceedings, pp. 294–304. IEEE (2000)
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. IACR Cryptology ePrint Archive 2017, 330 (2017). http://eprint.iacr.org/2017/330
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_21
Katz, J., Ostrovsky, R., Smith, A.: Round efficiency of multi-party computation with a dishonest majority. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 578–595. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_36
Khurana, D., Sahai, A.: How to achieve non-malleability in one or two rounds. IACR Cryptology ePrint Archive 2017, 291 (2017). http://eprint.iacr.org/2017/291
Lapidot, D., Shamir, A.: Publicly verifiable non-interactive zero-knowledge proofs. In: Menezes, A.J., Vanstone, S.A. (eds.) CRYPTO 1990. LNCS, vol. 537, pp. 353–365. Springer, Heidelberg (1991). doi:10.1007/3-540-38424-3_26
Lin, H., Pass, R., Soni, P.: Two-round concurrent non-malleable commitment from time-lock puzzles. IACR Cryptology ePrint Archive 2017, 273 (2017). http://eprint.iacr.org/2017/273
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_26
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: Proceedings of the Twelfth Annual Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001, pp. 448–457 (2001)
Pandey, O., Pass, R., Vaikuntanathan, V.: Adaptive one-way functions and applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 57–74. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_4
Pass, R.: Bounded-concurrent secure multi-party computation with a dishonest majority. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004, pp. 232–241 (2004)
Pass, R., Wee, H.: Constant-round non-malleable commitments from sub-exponential one-way functions. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 638–655. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_32
Prabhakaran, M., Rosen, A., Sahai, A.: Concurrent zero knowledge with logarithmic round-complexity. In: FOCS, pp. 366–375 (2002)
Rabin, M.O.: How to exchange secrets with oblivious transfer. IACR Cryptology ePrint Archive 2005, 187 (2005)
Rosen, A.: A note on constant-round zero-knowledge proofs for NP. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 191–202. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24638-1_11
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, New York, NY, USA, 17–18 October 1999, pp. 543–553 (1999)
von-Ahn, L., Hopper, N., Langford, J.: Covert two-party computation. In: Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, pp. 513–522. ACM (2005)
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: FOCS, pp. 531–540 (2010)
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Acknowledgements
The third author would like to thank Yuval Ishai for describing ideas for constructing a four-round semi-honest MPC protocol using randomizing polynomials.
The first author was supported by grant 360584 from the Simons Foundation. The second and the third authors were supported in part by a DARPA/ARL Safeware Grant W911NF-15-C-0213.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Ananth, P., Choudhuri, A.R., Jain, A. (2017). A New Approach to Round-Optimal Secure Multiparty Computation. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)


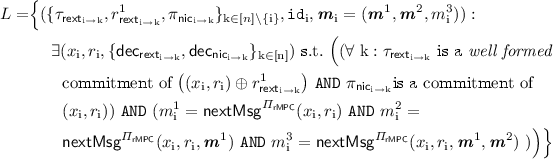
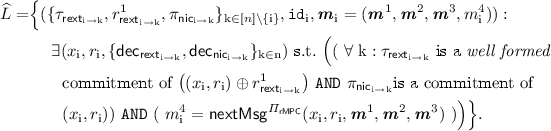
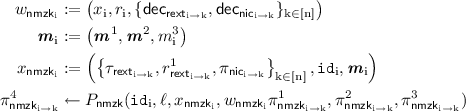
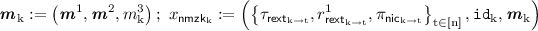
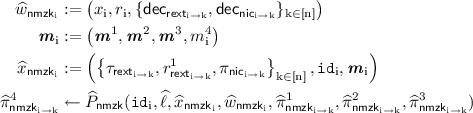
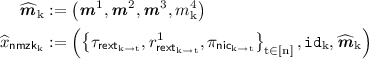
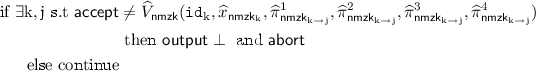


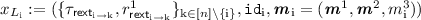 .
. 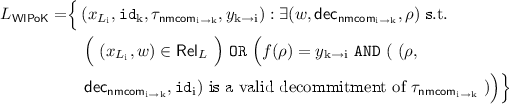
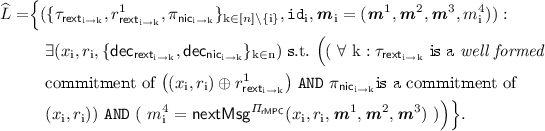
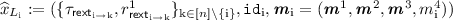 .
.