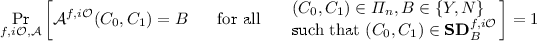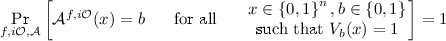Structure vs. Hardness Through the Obfuscation Lens

Abstract

Much of modern cryptography, starting from public-key encryption and going beyond, is based on the hardness of structured (mostly algebraic) problems like factoring, discrete log or finding short lattice vectors. While structure is perhaps what enables advanced applications, it also puts the hardness of these problems in question. In particular, this structure often puts them in low complexity classes such as ${\textsf {NP}} \cap {\textsf {coNP}}$ or statistical zero-knowledge (SZK).

Is this structure really necessary? For some cryptographic primitives, such as one-way permutations and homomorphic encryption, we know that the answer is yes—they imply hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ and ${\textsf {SZK}}$, respectively. In contrast, one-way functions do not imply such hard problems, at least not by fully black-box reductions. Yet, for many basic primitives such as public-key encryption, oblivious transfer, and functional encryption, we do not have any answer.

We show that the above primitives, and many others, do not imply hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ or ${\textsf {SZK}}$ via fully black-box reductions. In fact, we first show that even the very powerful notion of Indistinguishability Obfuscation (IO) does not imply such hard problems, and then deduce the same for a large class of primitives that can be constructed from IO.

MIT CSAIL. Research supported in part by NSF Grants CNS-1350619 and CNS-1414119, Alfred P. Sloan Research Fellowship, Microsoft Faculty Fellowship, the NEC Corporation, a Steven and Renee Finn Career Development Chair from MIT. This work was also sponsored in part by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226.

1 Introduction

The last four decades of research in cryptography has produced a host of fantastic objects, starting from one-way functions and permutations to public-key encryption [DH76, RSA78, GM82] and zero-knowledge proofs [GMR85] in the 1980s, all the way to fully homomorphic encryption [RAD78, Gen09, BV11] and indistinguishability obfuscation [BGI+01, GGH+13a] in the modern day.

The existence of all these objects requires at the very minimum that ${\textsf {NP}}\nsubseteq {\textsf {BPP}}$, but that is hardly ever enough. While one-way functions (OWFs), the most basic cryptographic object, does not seem to require much structure, as we advance up the ranks, we seem to require that certain structured problems are hard. For example, conjectured hard problems commonly used in cryptography (especially the public-key kind), such as factoring, discrete logarithms, and shortest (or closest) vectors on lattices all have considerable algebraic structure. On the one hand, it is this structure that enables strong applications such as public-key and homomorphic encryption. On the other hand, this structure is also what puts their hardness in question, and is exactly what algorithms may try to exploit in order to solve these problems. There is of course the fear that this structure will (eventually, if not today) deem these problems easy. Or, as Barak says more eloquently [Bar13]:

[...] based on the currently well studied schemes, structure is strongly associated with (and perhaps even implied by) public key cryptography. This is troubling news, since it makes public key crypto somewhat of an “endangered species” that could be wiped out by a surprising algorithmic advance. Therefore the question of whether structure is inherently necessary for public key crypto is not only of mathematical interest but also of practical importance as well.

Thus, a fundamental question in cryptography is what type of structure is necessary for different primitives? Indeed, the answer to this question may be crucial to our understanding of what are the minimal assumptions required to construct these primitives. While there may be different ways of approaching this question, one main approach, which is also taken in this work, has been through the eyes of complexity theory. That is, we wish to understand which cryptographic primitives require hardness in low (and so called structured) complexity classes such as ${\textsf {NP}} \cap {\textsf {coNP}}$, ${\textsf {TFNP}}$ (the class of total ${\textsf {NP}}$ search problems), or ${\textsf {SZK}}$ (the class of problems with statistical zero-knowledge proofs).

Aiming to answer this question, one line of research demonstrates that, for some cryptographic primitives, hardness in structured complexity classes is indeed necessary. The existence of one-way permutations (OWPs) requires a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$ [Bra79]; the same holds for restricted cases of public-key encryption schemes satisfying specific structural properties (e.g. ciphertext certification) [Bra79, GG98]; homomorphic encryption schemes and non-interactive computational private information retrieval schemes imply hard problems in ${\textsf {SZK}}$ [BL13, LV16]; and indistinguishability obfuscation schemes imply a hard problem in ${\textsf {PPAD}}\subseteq {\textsf {TFNP}}$ (assuming ${\textsf {NP}}\not \subseteq \mathsf{ioBPP}$) [BPR15].

Yet, for many primitives such hardness is not known to be inherent. While this is perhaps expected for OWFs, it is also the case for seemingly structured primitives such as collision-resistant hash functions, oblivious transfer, and general public-key encryption schemes. Do these primitives require hardness in structured complexity classes? Can we prove that they do or that they don’t?

Black-Box Separations. Formalizing this question in a meaningful way requires care. Indeed, it may be easy to formalize a statement of the form “the existence of crypto primitive $\mathcal {P}$ implies hardness in a complexity class $\mathcal {C}$”: one just needs to show a reduction from breaking $\mathcal {P}$ to solving problems in $\mathcal {C}$. However, it is not clear how to prove statements of the form “the existence of crypto primitive $\mathcal {P}$ does not imply hardness in a complexity class $\mathcal {C}$”. For example, it is commonly believed that ${\textsf {NP}} \cap {\textsf {coNP}}$ does contain hard problems. So in a trivial logical sense the existence of such problems is implied by any primitive $\mathcal {P}$. Instead, we follow the methodology of black-box separations, whose study in cryptography was pioneered by Impagliazzo and Rudich [IR89]. Faced with a similar problem of how to show that a primitive $\mathcal {P}$ (OWFs) cannot be used to construct another primitive $\mathcal {P}'$ (public-key encryption), they prove this cannot be shown through black-box reductions—cryptography’s de facto technique for showing such implications.

A bit more elaborately, a fully black-box reduction [RTV04] of a primitive (or, in our case, a problem) $\mathcal {P}'$ to a primitive $\mathcal {P}$ consists of a black-box construction and a black-box security reduction. The construction of $\mathcal {P}'$ from $\mathcal {P}$ does not exploit the actual implementation of primitive $\mathcal {P}$, but rather just its input-output interface. The security reduction can use any adversary that breaks (or, in our case, solves) $\mathcal {P}'$ to break $\mathcal {P}$, and is oblivious to the implementation of the adversary (as well as of that of $\mathcal {P}$).

Following [IR89], there has been a rich study of black-box separations in cryptography (see, e.g., [Rud91, Sim98, KST99, GKM+00, GT00, GMR01, BT03, RTV04, HR04, GGKT05, Pas06, GMM07, BM09, HH09, BKSY11, DLMM11, KSS11, GKLM12, DHT12, BBF13, Fis12, Pas13, BB15, HHRS15] and many others). Most of this study has been devoted to establishing separations between different cryptographic primitives. (In particular, the most relevant to us are the recent works of Asharov and Segev [AS15, AS16] that study black-box separations for indistinguishability obfuscation, which we elaborate on below.) Some of this study puts limitations on basing cryptographic primitives on NP-hardness [GG98, AGGM06, MX10, HMX10, BL13, BB15, LV16].

Going back to our main question of which primitives require structured hardness, we know the following.

• As described above, OWPs imply a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$ [Bra79], homomorphic encryption and PIR imply hard problems in ${\textsf {SZK}}$ [BL13, LV16] and IO (with OWFs) implies a hard problem in ${\textsf {PPAD}}$ [BPR15] via black-box reductions.

• On the flip side, we know that there are no black-box reductions from hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ to OWFs [BI87, Rud88], and from hard-on-average problems in ${\textsf {SZK}}$ to OWPs (corollary from [Ost91, OV08, HHRS15]).

For more advanced primitives, most notably (general) public-key encryption, we do not have results in either direction. In fact, many existing constructions are based on problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ or ${\textsf {SZK}}$. We are thus left with (quite basic) primitives at an unclear state; as far as we know, they may very well imply hard problems in structured complexity classes, even by black-box reductions.

1.1 Our Results

We revisit the relationship between two structured complexity classes, statistical zero-knowledge (${\textsf {SZK}}$) and ${\textsf {NP}} \cap {\textsf {coNP}}$, and cryptographic primitives. In broad strokes, we show that there are no fully black-box reductions of hard problems in these classes to any one of a variety of cryptographic primitives, including (general) public-key encryption, oblivious transfer, deniable encryption, and functional encryption. More generally, we separate ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ from indistinguishability obfuscation (IO). Then, leveraging on the fact that IO can be used to construct a wide variety of cryptographic primitives in a black-box way, we derive corresponding separations for these primitives.¹ One complexity-theoretic corollary of this result is a separation between ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ from the class ${\textsf {PPAD}}$ [MP91] that captures the complexity of computing Nash Equilibria.

On the positive side, we construct collision-resistant hash functions from a strong form of ${\textsf {SZK}}$-hardness and IO. It was previously known [AS15] that IO by itself does not imply collision-resistant hashing in a black-box way; we show that it does if one adds ${\textsf {SZK}}$-hardness as a “catalyst”.

We now go into more detail on each of the results.

Statistical Zero-Knowledge and Cryptography. The notion of statistical zero-knowledge proofs was introduced in the seminal work of Goldwasser et al. [GMR85]. The class of promise problems with statistical zero-knowledge proofs (SZK) can be characterized by several complete problems, such as statistical difference [SV03] and entropy difference [GV99]. ${\textsf {SZK}}$ hardness is known to follow from various number-theoretic problems that are commonly used in cryptography, such as Discrete Logarithms [GK93], Quadratic Residuosity [GMR85], Lattice Problems [GG98, MV03] as well as problems like Graph Isomorphism [GMW91]. As mentioned, we also know that a handful of cryptographic primitives such as homomorphic encryption [BL13], private information retrieval [LV16] and rerandomizable encryption imply hardness in ${\textsf {SZK}}$. (On the other hand, ${\textsf {SZK}}\subseteq {\textsf {AM}}\cap {\textsf {coAM}}$ [For89, AH91], and thus, ${\textsf {SZK}}$ cannot contain ${\textsf {NP}}$-hard problems, unless the polynomial hierarchy collapses [BHZ87].)

We ask more generally which cryptographic primitives can be shown to imply such hardness, with the intuition that such primitives are structured in a certain way. In particular, whereas one may not expect a seemingly unstructured object like OWFs to imply such hardness, what can we say for instance about OWPs, public-key encryption, or even IO (which has proven to be powerful enough to yield almost any known cryptographic goal)?

We prove that none of these primitives imply such hardness through black-box reductions.

Theorem 1.1

(Informal). There is no fully black-box reduction of any (even worst-case) hard problem in ${\mathsf {SZK}}$ to IO and OWPs.

Corollary 1.2

(from [SW14, Wat15], Informal). There is no such reduction to (general) public-key encryption, oblivious transfer, deniable encryption, functional encryption, or any other object that has a black-box reduction to IO and OWPs.

We would like to elaborate a bit more on what a black-box construction of a hard problem in ${\textsf {SZK}}$ means. We shall focus on the characterization of ${\textsf {SZK}}$ by the statistical difference promise problem [SV03]. In this problem, an instance is a pair of circuit samplers $C_0,C_1:\left\{ 0,1\right\} ^n\rightarrow \left\{ 0,1\right\} ^m$ which induce distributions $\varvec{C}_0$ and $\varvec{C}_1$ where the distribution $\varvec{C}_b$ obtained by evaluating the circuit $C_b$ on a uniformly random input. The promise is that the statistical distance $s=\mathsf {\Delta }(\varvec{C}_0,\varvec{C}_1)$ of the corresponding distributions is either large (say, $s\ge 2/3$) or small (say, $s\le 1/3$). The problem, named $\mathbf {SD}^{1/3,2/3}$ (or just $\mathbf {SD}$), is to decide which is the case.

Let us look at a specific example of the construction of such a problem from rerandomizable encryption. In a (say, symmetric-key) rerandomizable encryption scheme, on top of the usual encryption and decryption algorithms $({\textsf {Enc}},{\textsf {Dec}})$ there is a ciphertext rerandomization algorithm ${\textsf {ReRand}}$ that can statistically refresh ciphertexts. Namely, for any ciphertext ${\textsf {CT}}$ encrypting a bit b, ${\textsf {ReRand}}({\textsf {CT}})$ produces a ciphertext that is statistically close to a fresh encryption ${\textsf {Enc}}_{{\textsf {sk}}}(b)$. This immediately gives rise to a hard statistical difference problem [BL13]: given a pair of ciphertexts $({\textsf {CT}}_0,{\textsf {CT}}_1)$, decide whether the corresponding rerandomized distributions given by the circuits $(C_0(\cdot ),C_1(\cdot )):=({\textsf {ReRand}}({\textsf {CT}}_0;\cdot ),{\textsf {ReRand}}({\textsf {CT}}_1;\cdot ))$ are statistically far or close. Indeed, this corresponds to whether they encrypt the same bit or not, which is hard to decide by the security of the encryption scheme.

A feature of this reduction of hard statistical difference instances to rerandomizable encryption is that, similarly to most reductions in cryptography, it is fully black-box [RTV04] in the sense that the circuits $C_0,C_1$ only make black-box use of the encryption scheme’s algorithms, and can in fact be represented as oracle-aided circuits $(C_0^{{\textsf {ReRand}}(\cdot )},C_1^{{\textsf {ReRand}}(\cdot )})$. Furthermore, “hardness” can be shown by a black-box security proof that can use any decider for the problem in a black-box way to break the underlying encryption scheme. More generally, one can consider the statistical difference problem relative to different oracles implementing different cryptographic primitives and ask when can hardness be shown based on a black-box reduction. Theorem 1.1 rules out such reductions relative to IO and OWPs (and everything that follows from these in a fully black-box way). For more details, see Sect. 1.2 and the full version.

${\textsf {NP}} \cap {\textsf {coNP}}$ and Cryptography. Hard (on average) problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ are known to follow based on several number-theoretic problems in cryptography, such as Discrete Log, Factoring and Lattice Problems [Has88, LLJS90, AR04]. As in the previous section for ${\textsf {SZK}}$, we are interested in understanding which cryptographic primitives would imply such hardness, again with the intuition that this implies structure. For instance, it is known [Bra79] that any OWP $f:\left\{ 0,1\right\} ^n\rightarrow \left\{ 0,1\right\} ^n$ implies a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$, e.g. given an index $i \in [n]$ and an image f(x) find the ith preimage bit $x_i$. In contrast, Blum and Impagliazzo [BI87] and Rudich [Rud88] proved that seemingly unstructured objects like OWFs do not imply hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$ by fully black-box reductions. In this context, a fully black-box reduction essentially means that the non-deterministic verifiers only make black-box use of the OWF (or OWP in the previous example) and the reduction establishing the hardness is also black-box (in both the decider and the OWF).²

But what about more structured primitives such as public-key encryption, oblivious transfer, or even IO? We rule out fully black-box reductions from OWFs (or even injective OWFs) and IO to hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$. Hence, also for the other primitives, which can be constructed from IO (with OWFs) in a fully black-box way.

Theorem 1.3

(Informal). There is no fully black-box reduction of any (even worst-case) hard problem in ${\mathsf {NP}} \cap {\mathsf {coNP}}$ to IO and OWFs.

Corollary 1.4

(from [SW14, Wat15] Informal). There is no such reduction to (general) public-key encryption, oblivious transfer, deniable encryption, functional encryption, or any other object that has a black-box reduction to IO and OWFs.

Our approach also gives a new (rather different) proof to the original separation between OWFs and ${\textsf {NP}} \cap {\textsf {coNP}}$ [BI87, Rud88]. For more details, see Sect. 1.2 and the full version.

We remark that unlike our result for ${\textsf {SZK}}$ (which ruled out hard promise problems), the above result only rules out hard languages in ${\textsf {NP}} \cap {\textsf {coNP}}$. Indeed, Even et al. [ESY84] demonstrated promise problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ that are ${\textsf {NP}}$-hard. Hence even the assumption ${\textsf {P}}\ne {\textsf {NP}}$ (let alone OWFs) gives us hard promise problems in ${\textsf {NP}} \cap {\textsf {coNP}}$. (See [Gol06] for further reading.)

Relation to the Work of Asharov and Segev.The flood of IO applications following, starting from [GGH+13b, SW14], has lead many to conjecture that IO may be “complete for cryptography” (assuming also OWFs, or just ${\textsf {NP}}\not \subseteq \mathsf{ioBBP}$ [KMN+14]). Nevertheless, some cryptographic goals could not be constructed based on IO.

Asharov and Segev [AS15, AS16] were the first to initiate a formal study to understand the limits of IO. Our separations for IO are based on their framework [AS15]. We aim to draw the complexity-theoretic boundaries of IO. Indeed, black-box separations from IO require some care, given that the typical use of IO makes non-black-box use of the circuits it obfuscates and thus any associated cryptographic primitive such as OWFs. The Asharov-Segev framework considers obfuscators that take as input circuits with OWF (or OWP) gates. They observe, most known IO-based constructions fall into this category. Thus, a separation in this model allows deriving the corresponding separations between ${\textsf {SZK}}$ or ${\textsf {NP}} \cap {\textsf {coNP}}$ and a wide variety of cryptographic primitives. See Sect. 1.2 for more details.

In terms of results, they show that collision-resistant hashing and (domain invariant) OWPs do not have black-box reductions to IO (and OWFs). Our separation of IO and ${\textsf {NP}} \cap {\textsf {coNP}}$ is more general and implies their previous result for OWPs (and gives a rather different proof for this fact). Their result for collision-resistant hashing is not captured by our results (indeed collision-resistance is not known to imply hardness in either ${\textsf {SZK}}$ or ${\textsf {NP}} \cap {\textsf {coNP}}$). We also stress that our separation of ${\textsf {SZK}}$ from IO and OWPs does not follow from their results; indeed, SZK-hardness is not known to imply collision-resistance.³

Indistinguishability Obfuscation: Perspective. Since the breakthrough of [GGH+13b], the notion of IO has been extensively studied. While we already understand that IO has far reaching implications, our understanding of how it can be constructed and under what assumptions is still at an early stage. Indeed, basing IO on solid foundations is one of cryptography’s greatest challenges today. In this context, we stress that the results presented in this work hold regardless of the state of existing candidates. In fact, even if it turned out that there is no secure realization of IO, the separation of ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ from primitives such as public-key encryption, which follow from IO, still holds. The expressiveness of IO (established in [GGH+13b, SW14] and onwards) allows us to prove many separations in one shot. (Indeed, three years ago we would have probably addressed each primitive separately.)

As for the search for candidates itself, while at this point candidates are based on lattice-related problems that do break in SZK, our work suggests the theoretical possibility that IO candidates may not require such structure. A similar conclusion is true of course for the much more basic and long-studied question of public-key encryption. Almost all known public-key encryption candidates rely on very algebraic assumptions (that do break in ${\textsf {SZK}}$ or ${\textsf {NP}} \cap {\textsf {coNP}}$). Constructing public key encryption from less structured assumptions remains a fascinating open question. While there has been initial steps trying to diverge from such structure [Ale03, ABW10], there is yet a long way to go.

On ${\textsf {TFNP}}$ vs. ${\textsf {NP}} \cap {\textsf {coNP}}$. One of the corollaries of our result is a separation between ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ from the complexity class ${\textsf {PPAD}}$. ${\textsf {PPAD}}$, a subclass of total ${\textsf {NP}}$ search problems called ${\textsf {TFNP}}$ [MP91], was defined by Papadimitriou [Pap94] and has been shown to capture the complexity of computing Nash equilibria [DGP06, CDT09]. It was recently shown [BPR15] that IO and injective OWFs can be used (in a black-box way) to construct hard problems in ${\textsf {PPAD}}$. Put together with our separation, we get that there is no black-box construction of an ${\textsf {SZK}}$ (resp. ${\textsf {NP}} \cap {\textsf {coNP}}$) hard problem from ${\textsf {PPAD}}$-hardness.⁴

Given that ${\textsf {TFNP}}$, which contains ${\textsf {PPAD}}$, is commonly thought of as a search version of ${\textsf {NP}} \cap {\textsf {coNP}}$, it is interesting to note that the result shows that hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$ (of decisional problems) does not follow from hardness in ${\textsf {TFNP}}$ (aka, hardness of search problems) in a black-box way. Namely, there is no black-box “search-to-decision reduction” between these classes.

The Positive Result: Collision-Resistant Hashing from Strong ${\textsf {SZK}}$ -Hardness. We end our paper with a positive result. While most of our focus has been on showing that hardness in ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ does not follow from cryptography, here we ask the “inverse question”, namely whether certain cryptographic primitives can be built from other cryptographic primitives together with hardness in certain structured complexity classes. Little is known in this direction with the exception of the beautiful work of Ostrovsky [Ost91] which constructs a OWF from average-case ${\textsf {SZK}}$-hardness, and the recent work of Applebaum and Raykov [AR16] who showed that average-case hardness in the subclass $\mathsf {PRE}\subseteq \mathsf {SRE}\subseteq {\textsf {SZK}}$ of languages with a perfect randomized encoding gives us collision-resistant hashing.

We construct collision-resistant hashing from a strong form of ${\textsf {SZK}}$-hardness and IO. It was previously known [AS15] that IO by itself does not imply collision-resistant hashing in a black-box way; we show that it does if one adds ${\textsf {SZK}}$-hardness as a “catalyst”. Slightly more precisely, in the ${\textsf {SZK}}$-complete problem $\mathbf {SD}^{1/3,2/3}$ is required to distinguish between distributions that are 1 / 3-close from ones that are 2 / 3-far. We show that IO together with average-case hardness of $\mathbf {SD}^{0,1}$ (a stronger assumption) implies collision-resistant hashing.

Theorem 1.5

(Informal). Assuming average-case hardness of $\mathbf {SD}^{0,1}$ and the existence of IO, there is a collision-resistant hashing scheme.

Organization. Due to the paucity of space, most of the proofs are deferred to the full version. We give an overview of the methodology and techniques used in the following Sect. 1.2. The black-box separation between ${\textsf {SZK}}$ and IO (plus OWPs) is stated in Sect. 2. The separation between ${\textsf {NP}} \cap {\textsf {coNP}}$ and IO (plus injective OWFs) is described in Sect. 3.

1.2 Overview of Techniques

We now give an overview of our approach and main ideas. We start by discussing how to capture fully black-box constructions in the context of indistinguishability obfuscation following [AS15]. We then recall the common methodology for ruling out black-box constructions [IR89, RTV04, BBF13], and explain the main ideas behind our impossibility results for ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$. In the last part of this section, we outline the construction of collision-resistant hashing from indistinguishability obfuscation and ${\textsf {SZK}}$-hardness and the main ideas behind it.

Indistinguishability Obfuscation and Black-Box Constructions. Traditionally, when thinking about a black-box construction of one cryptographic primitive $\mathcal {P}'$ (e.g., a pseudo-random generator) from a primitive $\mathcal {P}$ (e.g., a one-way function), we mean that all algorithms in the construction of $\mathcal {P}'$ invoke $\mathcal {P}$ as a black-box, oblivious of its actual implementation. This is hardly the case in constructions based on indistinguishability obfuscation where circuits that explicitly invoke the primitive $\mathcal {P}$ may be obfuscated.

Nonetheless, as observed by Asharov and Segev [AS15], in almost all existing constructions, the code implementing $\mathcal {P}$ is used in a very restricted manner. Typically, obfuscated circuits can be implemented as oracle aided circuits $C^{\mathcal {P}}$ that are completely black-box in $\mathcal {P}$, where $\mathcal {P}$ is some low-level primitive, such as a one-way function. Indeed, in most cases the circuits obfuscated are symmetric-key primitives, such as puncturable pseudo-random functions [SW14], which can be constructed in a black-box way from one-way functions (in some constructions more structured low-level primitives may be used, like injective one-way functions, or one-way permutations). Furthermore, in these constructions, the obfuscator $i\mathcal {O}$ itself is also treated as a black-box.

Accordingly, almost all existing constructions based on indistinguishability obfuscation can be cast into a model in which indistinguishability obfuscation exists for oracle-aided circuits $C^{\mathcal {P}}$, where $\mathcal {P}$ is say a one-way function, and both $\mathcal {P}$ and the obfuscator $i\mathcal {O}$ can only be accessed as black-boxes. On top of that, they can be proven secure in this model by a black-box reduction that makes black-box use of $(\mathcal {P}, i\mathcal {O})$ and any attacker against the constructed primitive $\mathcal {P}'$. Such constructions where both the construction itself and the reduction are black-box are called fully black-box constructions [RTV04]. Following Asharov and Segev [AS15, AS16], we shall prove our results in this model, ruling out black-box constructions of hard problems in ${\textsf {SZK}}$ and ${\textsf {NP}} \cap {\textsf {coNP}}$ based on indistinguishability obfuscation for oracle-aided circuits. Further details follow.

Ruling out Black-Box Reductions. We prove our results in the model described above following the methodology of oracle separations (see e.g. [IR89, Sim98, RTV04, HR04]). Concretely, to prove that there is no fully black-box construction of a primitive $\mathcal {P}'$ from primitive $\mathcal {P}$, we demonstrate oracles $(\varPsi ,\mathcal {A})$ such that:

• relative to $\varPsi$, there exists a construction $C_{\mathcal {P}}^{\varPsi }$ realizing $\mathcal {P}$ that is secure in the presence of $\mathcal {A}$,

• but any construction $C_{\mathcal {P}'}^{\varPsi }$ realizing $\mathcal {P}'$ can be broken in the presence of $\mathcal {A}$.

Indeed, if such oracles $(\varPsi ,\mathcal {A})$ exist, then no efficient reduction will be able to use (as a black-box) the attacker $\mathcal {A}$ against $\mathcal {P}'$ to break $\mathcal {P}$ (as the construction of $\mathcal {P}$ is secure in the presence of $\mathcal {A}$). In our case, we would like to apply this paradigm rule out black-box constructions of hard instances in either ${\textsf {SZK}}$ or ${\textsf {NP}} \cap {\textsf {coNP}}$ from a low-level primitive (e.g. a one-way function) indistinguishability obfuscation for oracle-aided circuits. We next outline the main ideas behind the construction and analysis of the oracles $(\varPsi ,\mathcal {A})$ in each of the two cases.

Ruling out Black-Box Constructions of Hard ${\textsf {SZK}}$ Problems. As explained in the previous section, we focus on the characterization of ${\textsf {SZK}}$ by its complete problem: the statistical difference problem $\mathbf {SD}$ [SV03]. We demonstrate oracles $(\varPsi ,\mathcal {A})$ such that relative to $\varPsi$ there exist constructions of one-way permutations (OWPs) and IO for circuits with OWP gates, and these constructions are secure in the presence of $\mathcal {A}$. At the same time, $\mathcal {A}$ will decide (in the worst-case) $\mathbf {SD}^{\varPsi }$. Since $\mathbf {SD}$ is complete for ${\textsf {SZK}}$ in a relativizing manner, deciding $\mathbf {SD}^\varPsi$ suffices to break ${\textsf {SZK}}^\varPsi$. That is, $\mathcal {A}$ will decide all instances $(C_0^{\varPsi },C_1^{\varPsi })$ of circuit samplers that only use the IO and OWPs realized by $\varPsi$ in a black-box manner. We next explain how each of the two are constructed.

The construction of $\varPsi$ follows a general recipe suggested in [AS15, AS16]. The oracle consists of three parts where:

• 1. $f$ is a random permutation, realizing the one-way permutation primitive.

• 2. $\mathcal {O}$ is a random injective function, realizing the obfuscation algorithm. It takes as input an oracle-aided circuit $C^{(\cdot )}$ along with randomness r and outputs an obfuscation ${\widehat{C}} = \mathcal {O}(C,r)$.

• 3. realizes evaluation of obfuscated circuits. On input $({\widehat{C}},x)$, it inverts $\mathcal {O}$ to find (C, r), and outputs $C^ f (x)$. If ${\widehat{C}}$ is not in the image of $\mathcal {O}$, it returns $\bot$.

The above construction readily satisfies the syntactic (or “functionality”) requirements of one-way permutations and indistinguishability obfuscation. Furthermore, using standard techniques, it is not hard to show that relative to $\varPsi$, the function $f$ is one-way and $\mathcal {O}$ satisfies IO indistinguishability requirement. The challenge is to now come up with an oracle $\mathcal {A}$ that, on one hand, will decide $\mathbf {SD}^\varPsi$, but on the other, will not compromise the security of the latter primitives.

Recall that deciding $\mathbf {SD}^{\varPsi }$ means that given two oracle-aided circuit samplers $(C_0,C_1)$ such that the statistical distance of the corresponding distributions $(\varvec{C}_0^{\varPsi },\varvec{C}_1^{\varPsi })$ is $s=\mathsf {\Delta }(\varvec{C}_0^{\varPsi },\varvec{C}_1^{\varPsi })\in [0,\frac{1}{3}]\cup [\frac{2}{3},1]$, the oracle $\mathcal {A}$ must decide in which of the two intervals s lies, whereas if the promise is not satisfied and $s\in (\frac{1}{3},\frac{2}{3})$, there is no requirement whatsoever. With this in mind, a first naive attempt would be the following. $\mathcal {A}$ will have unbounded access to $\varPsi$, give a query $(C_0,C_1)$, it would compute $s=\mathsf {\Delta }(\varvec{C}_0,\varvec{C}_1)$, and simply say whether $s<\frac{1}{2}$ or $s\ge \frac{1}{2}$. While such an oracle would definitely decide $\mathbf {SD}^\varPsi$, it is not too hard to show that it is simply too powerful, and would not only break IO and OWPs, but would, in fact, allow solving any problem in ${\textsf {NP}}^\varPsi$ (or even in ${\mathsf {PP}}^{\varPsi }$). Other naive attempts such as refusing to answer outside the promise intervals, encounter a similar problem.

At high-level, the problem with such oracles is that solutions to hard problems can be easily correlated with “tiny” differences in the statistical distance of the two input circuits, whereas the above oracle may reflect tiny changes when the statistical distance is close to some threshold (1 / 2 in the above example) on which the oracle changes its behaviour. This motivates our actual definition of $\mathcal {A}$ as a noisy oracle that produces its answer, not according to some fixed threshold, but according to a random threshold, chosen afresh for each and every query. Concretely, the oracle, which we call ${\mathsf {\mathsf {StaDif}}}^\varPsi$, for any query $(C_0,C_1)$, chooses a uniformly random threshold $t\leftarrow (\frac{1}{3},\frac{1}{3})$, and answers accordingly:

$${\mathsf {\mathsf {StaDif}}}^{\varPsi }(C_0,C_1) = {\left\{ \begin{array}{ll} Y &{} \text {if } s \ge t \text { (far distributions)}\\ N &{} \text {if } s < t \text { (similar distributions)}\end{array}\right. }.$$

The main challenge in proving that the security of the IO and OWPs realized by $\mathcal {A}$ is not compromised by this oracle is that ${\mathsf {\mathsf {StaDif}}}^{\varPsi }$ has the power to query $\varPsi$ on exponentially many points in order to compute s. For instance, it may query $\varPsi$ on the preimage of a OWP challenge $f (x)$ or of a given obfuscation ${{\mathcal {O}}}(C,r)$. The key observation behind the proof is that the oracle’s final answer still does not reflect how $\varPsi$ behaves locally on random points.

Intuitively, choosing the threshold t at random, for each query $(C_0,C_1)$, guarantees that with high probability t is “far” from the corresponding statistical distance $s=\mathsf {\Delta }(C_0^{\varPsi },C_1^{\varPsi })$. Thus, changing the oracle $\varPsi$ on, say, a single input x, such as the preimage of an OWP challenge $f (x)$, should not significantly change s and will not affect the oracle’s answer; that is, unless the circuits query $\varPsi$ on x with high probability to begin with. We give a reduction showing that we can always assume that $(C_0,C_1)$ are “smooth”, in the sense that they do not make any specific query to $\varPsi$ with too high probability.

Following this intuition, we are able to show that through such local changes that go undetected by ${\mathsf {\mathsf {StaDif}}}^{\varPsi }$, we can move to an ideal world where inverting the OWP or breaking IO can be easily shown to be impossible. We refer the reader to the full version for further details.

Ruling out Black-Box Constructions of Hard ${\textsf {NP}} \cap {\textsf {coNP}}$ Problems. As mentioned earlier, a fully black-box construction of hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ is actually known assuming one-way permutations (OWPs), and cannot be ruled out as in the case of ${\textsf {SZK}}$. Instead, we rule out constructions from (non-surjective) injective one-way functions (IOWFs) and IO for circuits with IOWF gates. This generalizes several previous results by Blum and Impagliazzo [BI87] and Rudich [Rud88], showing that OWFs do not give hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$, by Matsuda and Matsuura [MM11], showing that IOWFs do not give OWPs (which are a special case of hardness ${\textsf {NP}} \cap {\textsf {coNP}}$), and by Asharov and Segev [AS16], showing that OWFs and IO for circuits with OWF gates do not give OWPs. In fact, our approach yields a new (and rather different) proof for each one of these results.

We follow a similar methodology to one we used for the case of ${\textsf {SZK}}$. That is, we would like to come up with oracles $(\varPsi ,\mathcal {A})$ such that $\varPsi$ realizes IOWFs and IO for circuits with IOWFs gates, which are both secure in the presence of $\mathcal {A}$, whereas black-box constructions of problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ from these primitives can be easily solved by $\mathcal {A}$. By black-box constructions here we mean a pair of efficient oracle-aided non-deterministic verifiers $V_0^{(\cdot )},V_1^{(\cdot )}$ that for every oracle $\varPsi$ implementing IOWFs and IO, yield co-languages $\overline{L}^{\varPsi },L^{\varPsi }$ in ${\textsf {NP}} \cap {\textsf {coNP}}[\varPsi ]$.

The requirement that $V_0,V_1$ give a language in ${\textsf {NP}} \cap {\textsf {coNP}}$ for every oracle implementing IOWFs and IO follows previous modeling [BI87],⁵ and aligns with how we usually think about correctness of black-box constructions of cryptographic primitives. For instance, the construction of public-key encryption from trapdoor permutations is promised to be correct, for all oracles implementing the trapdoor permutation. Similarly, the construction of hard ${\textsf {NP}} \cap {\textsf {coNP}}$ languages from one-way permutations, give an ${\textsf {NP}} \cap {\textsf {coNP}}$ language for any oracle implementing a permutation.⁶

We stress that a construction where correctness is only guaranteed for particular (even if natural) oracles may definitely exist. This is for example the case if we only consider implementations of IO similar to those presented above in the context of ${\textsf {SZK}}$. Indeed, in that construction the implementation of IO has an additional property—it allows identifying invalid obfuscations (the oracle would simply return $\bot$ on such obfuscations). This “verifiability” property coupled with the injectivity of obfuscators actually imply a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$ in a black-box way.⁷ Our separation thus leverages the fact that IO need not necessarily be verifiable, and rules out constructions that are required to be correct for any implementation of IO, even a non-verifiable one.

Accordingly, the oracles that we consider are a tweaked version of the oracles considered in the ${\textsf {SZK}}$ case. Now ${{f}}$ is a random injective function that is expanding, rather than a permutation, the oracle ${{\mathcal {O}}}$ is defined as before, and the oracle is defined as before for valid obfuscations but is allowed to act arbitrarily for invalid obfuscations. As for $\mathcal {A}$, this time it is trivially implemented by an oracle $\mathsf {Decide}^\varPsi$ that, given input x, simply returns the unique bit b such that $V_b(x)=1$, namely it just decides the corresponding language $L^\varPsi$.

In the results mentioned above [Rud88, MM11, AS16], it is actually shown that any query to such an oracle can be completely simulated with a small number of queries to $\varPsi$.⁸ We do not show such a simulation process. Instead, we take a different approach inspired by our proof for the ${\textsf {SZK}}$ setting described above. Roughly speaking, we show that somewhat similarly to our statistical difference oracle ${\mathsf {\mathsf {StaDif}}}^{\varPsi }$, the oracle $\mathsf {Decide}^{\varPsi }$ is also rather robust to random local changes. The main observation here is that for any fixed yes-instance $x\in L^{\varPsi }$, tweaking $\varPsi$ at a random input into a new oracle $\varPsi '$, it is likely that x will still be a yes-instance in $L^{\varPsi '}$, as long as $\varPsi '$ is in our allowed family of oracles and $L^{\varPsi '}$ is indeed in ${\textsf {NP}} \cap {\textsf {coNP}}[\varPsi ']$ (and the same is true for no-instances).

In slightly more detail, fixing a witness w such that $V_1^{\varPsi }(x,w) = 1$, we can show that since $V_1$ makes a small number of oracle calls, with high probability tweaking the oracle $\varPsi$ at a random place will not affect these oracle calls and thus $V_1^{\varPsi '}(x,w) = V_1^{\varPsi }(x,w)=1$. Then, assuming $L^{\varPsi '}$ is guaranteed to be in ${\textsf {NP}} \cap {\textsf {coNP}}$, we can deduce that x must still a yes-instance (other witnesses for this fact may be added or disappear, but this does not change the oracle’s answer). In the body, we argue that indeed $L^{\varPsi '}\in {\textsf {NP}} \cap {\textsf {coNP}}[\varPsi ']$, where we strongly rely on the fact that arbitrary behavior of is permitted on invalid obfuscations.

Once again, we show that through local changes that go undetected by $\mathsf {Decide}^{\varPsi }$, we can move to an ideal world where inverting the IOWF or breaking IO can be easily shown to be impossible. We refer the reader to Sect. 3 for further details.

Implied Separations. As a result of the two separations discussed above, we can rule out black-box constructions of hard problems in ${\textsf {SZK}}$ or ${\textsf {NP}} \cap {\textsf {coNP}}$ from various cryptographic primitives or complexity classes. This essentially includes all primitives that have fully black-box constructions from OWPs (or IOWFs) and IO for circuits with OWP (or IWOF) gates. This includes public-key encryption, oblivious transfer, deniable encryption [SW14], functional encryption [Wat15], delegation, [BGL+15, CHJV15, KLW15], hard (on-average) ${\textsf {PPAD}}$ instances [BPR15], and more.

We note that there a few applications of IO that do not fall under this characterization. For instance, the construction of IO for Turing machines from IO-based succinct randomized encodings [BGL+15, CHJV15, KLW15] involves obfuscating a circuit that itself outputs (smaller) obfuscated circuits. To capture this, we would need to extend the above model to IO for circuits that can also make IO oracle calls (on smaller circuits). Another example is the construction of non-interactive witness indistinguishable proofs from IO [BP15]. There an obfuscated circuit may get as input another obfuscated circuit and would have to internally run it; furthermore, in this application, the code of the obfuscator is used in a (non-black-box) ZAP. Extending the above model to account for this type of IO applications is an interesting question that we leave for future exploration.

The Positive Result: Collision-Resistance from IO and ${\textsf {SZK}}$ -Hardness. We now described the main ideas behind our construction of collision-resistant hash functions. The starting point for the construction is the work of Ishai et al. [IKO05] that shows how to construct collision-resistant hash functions from commitments that are additively homomorphic (for simplicity, say over $\mathbb {F}_2)$. The idea is simple: we can hash $\ell$ bits to m bits, where m is the size of a single bit commitment and $\ell$ can be arbitrarily longer, as follows. The hash key is a commitment $\gamma :=(\mathsf {com}(\beta _1),\dots ,\mathsf {com}(\beta _\ell ))$ to a random vector $\beta \in \mathbb {F}_2^{\ell }$, and hashing $x\in \mathbb {F}_2^\ell$, is done by homomorphically computing a commitment to the inner product $\mathsf{CRH}_{\gamma }(x) = \mathsf {com}(\langle \beta ,x\rangle )$. Intuitively, the reason this works is that any collision in $\mathsf{CRH}_{\gamma }$ reveals a vector that is orthogonal to $\beta$ and thus leaks information about it and violating the hiding of the commitment.

At a high-level, we aim to mimic the above construction based on obfuscation. As a key for the collision-resistant hash we can obfuscate a program $\varPi _{\beta }$ associated with a random vector $\beta$ that given x outputs a commitment $\mathsf {com}(\langle \beta ,x\rangle )$, where the commitment is derandomized using a PRF.⁹ The obfuscation $i\mathcal {O}(\varPi _{\beta })$ can be thought of as the commitment to $\beta$, and evaluating this program at x, corresponds to homomorphic evaluation. Despite the clear intuition behind this construction, it is not clear how to prove its security based on IO. In fact, by the work of Asharov and Segev [AS15], it cannot be proven based on a black-box reduction as long as plain statistically-binding commitments are used, as these can be constructed from OWPs in a fully black-box manner, and [AS15] rule out black-box constructions of collision-resistant hashing from OWPs and IO for circuits with OWP gates.

We show, however, that relying on a relaxed notion of perfectly-hiding commitments, as well as subexponential hardness of IO and puncturable PRFs, the construction can be proven secure. The perfect hiding of the commitment is leveraged in a probabilistic IO argument [CLTV15] that involves a number of hybrids larger than the overall number of commitments. We then observe that these relaxed commitments follow from average-case hardness of the polar statistical difference problem $\mathbf {SD}^{0,1}$.¹⁰

2 One-Way Permutations, Indistinguishability Obfuscation, and Hardness in SZK

In this section, we ask which cryptographic primitives imply hardness in the class statistical zero-knowledge (SZK). Roughly speaking, we show that one-way permutations (OWPs) and indistinguishability obfuscation (IO), for circuits with OWP-gates, do not give rise to a black-box construction of hard problems in ${\textsf {SZK}}$. This, in turn implies that many cryptographic primitives (e.g., public-key encryption, functional encryption, and delegation), and hardness in certain low-level complexity classes (e.g. ${\textsf {PPAD}}$), also do not yield black-box constructions of hard problems in ${\textsf {SZK}}$.

We first motivate and define a framework of ${\textsf {SZK}}$ relative to oracles, define fully black-box constructions of hard ${\textsf {SZK}}$ problems, and then move on to the actual separation.

2.1 SZK and Statistical Difference

The notion of statistical zero-knowledge proofs was introduced in the seminal work of Goldwasser et al. [GMR85]. The class of promise problems with statistical zero-knowledge proofs (SZK) can be characterized by several complete problems, such as statistical difference [SV03] and entropy difference [GV99] (see also [Vad99] and references within). We shall focus on the characterization of ${\textsf {SZK}}$ by the statistical difference problem. Here an instance is a pair of circuit samplers $C_0,C_1:\left\{ 0,1\right\} ^n\rightarrow \left\{ 0,1\right\} ^m$ with the promise that the statistical distance $s=\mathsf {\Delta }(\varvec{C}_0,\varvec{C}_1)$ of the corresponding distributions is either large (say, $s\ge 2/3$) or small (say, $s\le 1/3$). The problem is to decide which is the case.

Hard Statistical Difference Problems from Cryptography: Motivation. ${\textsf {SZK}}$ hardness, and in particular hard statistical difference problems, are known to follow from various number-theoretic and lattice problems that are commonly used in cryptography, such as Decision Diffie-Hellman, Quadratic Residuosity, and Learning with Errors. We ask more generally which cryptographic primitives can be shown to imply such hardness, with the intuition that such primitives are structured in a certain way. In particular, whereas one would not expect a completely unstructured object like one-way functions to imply such hardness, what can we say for instance about public-key encryption, or even indistinguishability obfuscation (which has proven to be structured enough to yield almost any known cryptographic goal).

We prove that none of these primitives imply such hardness through the natural class of black-box constructions and security reductions. To understand what a black-box construction of a hard statistical difference problem means, let us look at a specific example of the construction of such a problem from rerandomizable encryption. In a (say, symmetric-key) rerandomizable encryption scheme, on top of the usual encryption and decryption algorithms $({\textsf {Enc}},{\textsf {Dec}})$ there is a ciphertext rerandomization algorithm ${\textsf {ReRand}}$ that can statistically refresh ciphertexts. Namely, for any ciphertext ${\textsf {CT}}$ encrypting a bit b, ${\textsf {ReRand}}({\textsf {CT}})$ produces a ciphertext that is statistically close to a fresh encryption ${\textsf {Enc}}(b)$. Note that this immediately gives rise to a hard statistical difference problem: given a pair of ciphertexts $({\textsf {CT}},{\textsf {CT}}')$, decide whether the corresponding rerandomized distributions given by the circuits $(C_0(\cdot ),C_1(\cdot )):=({\textsf {ReRand}}({\textsf {CT}};\cdot ),{\textsf {ReRand}}({\textsf {CT}}';\cdot ))$ are statistically far or close. Indeed, this corresponds to whether they encrypt the same bit or not, which is hard to decide by the security of the encryption scheme.

A feature of this construction of hard statistical difference instances is that, similarly to most constructions in cryptography, it is fully black-box [RTV04] in the sense that the circuits $C_0,C_1$ only make black-box use of the encryption scheme’s algorithms, and can in fact be represented as oracle-aided circuits $(C_0^{{\textsf {ReRand}}(\cdot )},C_1^{{\textsf {ReRand}}(\cdot )})$. Furthermore, “hardness” can be shown by a black-box reduction that can use any decider for the problem in a black-box way to break the underlying encryption scheme. More generally, one can consider the statistical difference problem relative to different oracles implementing different cryptographic primitives and ask when can hardness be shown based on a black-box reduction. We will rule out such reductions relative to IO and OWPs (and everything that follows from these in a fully black-box way).

2.2 Fully Black-Box Constructions of Hard SD Problems from IO and OWPs

We start by defining statistical difference problem relative to oracles. In the following definition, for an oracle-aided (sampler) circuit $C^{(\cdot )}$ with n-bit input and an oracle $\varPsi$, we denote by $\varvec{C}^\varPsi$ the output distribution $C^\varPsi (r)$ where $r \leftarrow \left\{ 0,1\right\} ^n$. For two distributions $\mathbf {X}$ and $\mathbf {Y}$ we denote their statistical distance by $\mathsf {\Delta }(\mathbf {X},\mathbf {Y})$.

Definition 2.1

(Statistical difference relative to oracles). For an oracle $\varPsi$, the statistical difference promise problem relative to $\varPsi$, denoted as $\mathbf {SD}^{\varPsi }=(\mathbf {SD}_{Y}^{\varPsi }$, $\mathbf {SD}_{N}^{\varPsi })$, is given by

We now formally define the class of constructions and reductions ruled out. That is, fully black-box constructions of hard statistical distance problems from OWPs and IO for OWP-aided circuits. The definition is similar in spirit to those in [AS15, AS16], adapted to our context of ${\textsf {SZK}}$-hardness.

Definition 2.2

A fully black-box construction of a hard statistical distance problem from OWPs and IO for the class $\mathcal {C}$ of circuits with OWP-gates consists of a collection of oracle-aided circuit pairs $\varPi ^{(\cdot )}=\left\{ \varPi _n^{(\cdot )} = \left\{ (C_0^{(\cdot )},C_1^{(\cdot )})\in \left\{ 0,1\right\} ^{n\times 2}\right\} \right\} _{n\in \mathbb {N}}$ and a probabilistic oracle-aided reduction $\mathcal {R}$ that satisfy:

• Black-box security proof: There exist functions $q_\mathcal {R}(\cdot ), \varepsilon _\mathcal {R}(\cdot )$ such that the following holds. Let ${{f}}$ be any distribution on permutations and let ${{i\mathcal {O}}}$ be any distribution on functions such that ${\widehat{C}}^{{f}}\equiv C^{{f}}$ for any $C^{(\cdot )}$ and r, where ${\widehat{C}}^{(\cdot )}\,:=\,{{i\mathcal {O}}}(C^{(\cdot )},r)$. Then for any probabilistic oracle-aided $\mathcal {A}$ that decides $\varPi$ in the worst-case, namely, for all $n\in \mathbb {N}$

  

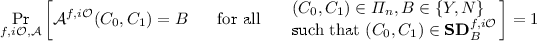
  the reduction breaks either ${{f}}$ or ${{i\mathcal {O}}}$, namely, for infinitely many $n\in \mathbb {N}$ either

  

  or

  

  where in both $\mathcal {R}$ makes at most $q_\mathcal {R}(n)$ queries to any of its oracles $(\mathcal {A},{{f}},{{i\mathcal {O}}})$, and any query $(C_0^{(\cdot )},C_1^{(\cdot )})$ it makes to $\mathcal {A}$ consists of circuits that also make at most $q_\mathcal {R}(n)$ queries to their oracles $({{f}},{{i\mathcal {O}}})$. The random variable ${\mathsf {Exp}}^{\mathsf {iO}}_{({{f}},{{i\mathcal {O}}}), {{i\mathcal {O}}}, \mathcal {C},\mathcal {R}^{\mathcal {A}}}(n)$ represents the reductions winning probability in the IO security game relative to $({{f}},{{i\mathcal {O}}})$.

We make several remarks about the definition:

• Correctness. Typically, we also require certain correctness from the black-box construction. For instance, in the next section, we shall require that the construction always satisfies the ${\textsf {NP}} \cap {\textsf {coNP}}$ structure. In the above definition, the construction is allowed to yield instances $(C_0^{{{f}},{{i\mathcal {O}}}},C_1^{{{f}},{{i\mathcal {O}}}})$ that do not satisfy the ${\textsf {SZK}}$ promise; namely $(C_0^{{{f}},{{i\mathcal {O}}}},C_1^{{{f}},{{i\mathcal {O}}}})\notin \mathbf {SD}_Y^{{{f}},{{i\mathcal {O}}}}\cup \mathbf {SD}_N^{{{f}},{{i\mathcal {O}}}}$. It is natural to think of more stringent definitions that require that the corresponding problem $\varPi ^{{{f}},{{i\mathcal {O}}}}$ is non-trivial, in the sense that $\varPi ^{{{f}},{{i\mathcal {O}}}}\,\cap \,\mathbf {SD}_Y^{{{f}},{{i\mathcal {O}}}}\,\ne \,\emptyset$ and $\varPi ^{{{f}},{{i\mathcal {O}}}}\,\cap \,\mathbf {SD}_N^{{{f}},{{i\mathcal {O}}}}\,\ne \,\emptyset$ (which is the case for known constructions of SZK hardness from cryptographic primitives). Our impossibility is more general and would, in particular, rule out such definitions as well.

• Worst-Case vs. Average-Case Hardness. In the above, we address worst-case hardness, in the sense that the reduction $\mathcal {R}$ has to break the underlying primitives only given a decider $\mathcal {A}$ that is always correct. One could further ask whether IO and OWPs even imply average-case hardness in ${\textsf {SZK}}$ (as do many of the algebraic hardness assumptions in cryptography). Ruling out worst-case hardness (as we will do shortly) in particular rules out such average-case hardness as well.

• IO for Oracle-Aided Circuits. Following [AS15, AS16], we consider indistinguishability obfuscation for oracle-aided circuits $C^{f}$ that can make calls to the one-way permutation oracle. This model captures constructions where IO is applied to circuits that use pseudo-random generators, puncturable pseudo-random functions, or injective one-way functions as all of those have fully black-box constructions from one-way permutations (see further discussion in [AS15]). This includes almost all known constructions from IO, including public-key encryption, deniable encryption [SW14], functional encryption [Wat15], delegation [BGL+15, CHJV15, KLW15], and hard (on-average) ${\textsf {PPAD}}$ instances [BPR15]. Accordingly, separating ${\textsf {SZK}}$ from IO and OWPs in this model, results in a similar separation between ${\textsf {SZK}}$ and any one of these primitives.

  We note that there a few applications though that do not fall under this model. The first is in applications where the obfuscated circuit might itself output (smaller) obfuscated circuit, for instance in the construction of IO for Turing machines from IO-based succinct randomized encodings [BGL+15, CHJV15, KLW15]. To capture such applications, one would have to extend the model to also account for circuits with IO gates (and not only OWP gates). A second example is the construction of non-interactive witness indistinguishable proofs from IO [BP15]. There an obfuscated circuit may get as input another obfuscated circuit and would have to internally run it; furthermore, in this application, the code of the obfuscator is used in a (non-black-box) ZAP. Extending our results (and those of [AS15, AS16]) to these models is an interesting question, left for future work.

• Security Loss. In the above definition the functions $q_\mathcal {R}$ and $\varepsilon _\mathcal {R}$ capture the security loss of the reduction. Most commonly in cryptography, the query complexity is polynomial $q_\mathcal {R}(n)=n^{O(1)}$ and the probability of breaking the underlying primitive is inverse polynomial $\varepsilon _{\mathcal {R}}(n) = n^{-O(1)}$. Our lower-bounds will in-fact apply for exponential $q_{\mathcal {R}},\varepsilon _{\mathcal {R}}^{-1}$. This allows capturing also constructions that rely on subexponentially secure primitives (e.g., [BGL+15, CHJV15, KLW15, BPR15, BPW16]).

Ruling Out Fully Black-Box Constructions: A Road Map. Our main result in this section is that a fully black-box construction of a hard statistical difference problem from IO and OWPs does not exist. Furthermore, this holds even if the latter primitives are exponentially secure.

Theorem 2.3

Any fully black-box construction of a statistical difference problem $\varPi$ from OWPs and IO for circuits with OWP gates has an exponential security loss: $\max (q_{\mathcal {R}}(n),\varepsilon _{\mathcal {R}}^{-1}(n)) \ge \varOmega (2^{n/12})$.

The proof of the theorem follows a common methodology (applied for instance in [HR04, HHRS15, AS15]). We exhibit two (distributions on) oracles $(\varPsi ,{\mathsf {\mathsf {StaDif}}}^{\varPsi })$, where $\varPsi$ realizes OWPs and IO for circuits with OWP gates, and ${\mathsf {\mathsf {StaDif}}}^{\varPsi }$ that decides $\mathbf {SD}^{\varPsi }$, the statistical difference problem relative to $\varPsi$, in the worst case. Since $\mathbf {SD}$ is complete for ${\textsf {SZK}}$ in a relativizing manner, solving $\mathbf {SD}^\varPsi$ suffices to break ${\textsf {SZK}}^\varPsi$. We then show that the primitives realized by $\varPsi$ are (exponentially) secure even in the presence of ${\mathsf {\mathsf {StaDif}}}^{\varPsi }$. Then viewing ${\mathsf {\mathsf {StaDif}}}$ as a worst-case decider $\mathcal {A}$ (as per Definition 2.2) directly implies Theorem 2.3, ruling out fully black-box constructions with a subexponential security loss. We defer the oracle description and the proof to the full version.

3 One-Way Functions, Indistinguishability Obfuscation, and Hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$

In this section, we show that injective one-way functions (IOWFs) and indistinguishability obfuscation (IO), for circuits with IOWF-gates, do not give rise to a black-box construction of hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$. This can be seen as a generalization of previous separations by Rudich [Rud88], showing that OWFs do not give hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$, by Matsuda and Matsuura [MM11], showing that IOWFs do not give one-way permutations (which are a special case of hardness ${\textsf {NP}} \cap {\textsf {coNP}}$), and by Asharov and Segev [AS16], showing that OWFs and IO do not give one-way permutations. As in the previous section, the result implies that many cryptographic primitives and hardness in ${\textsf {PPAD}}$, also do not yield black-box constructions of hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$.

We first define the framework of ${\textsf {NP}} \cap {\textsf {coNP}}$ relative to oracles, define fully black-box constructions of hard ${\textsf {NP}} \cap {\textsf {coNP}}$ problems, and then move on to the actual separation.

3.1 ${\textsf {NP}} \cap {\textsf {coNP}}$

Throughout, we shall canonically represent languages $L\in {\textsf {NP}} \cap {\textsf {coNP}}$ by their corresponding non-deterministic poly-time verifiers $V_1,V_0$, where

Hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$ from Cryptography - Motivation. Hard (on average) problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ are known to follow based on certain number-theoretic problems in cryptography, such as Discrete Log and Factoring. As in the previous section for ${\textsf {SZK}}$, we are interested in understanding which cryptographic primitives would imply such hardness, again with the intuition that these should be appropriately structured. For instance, it is known [Bra79] that any one-way permutation $f:\left\{ 0,1\right\} ^n\rightarrow \left\{ 0,1\right\} ^n$ implies a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$, e.g. given an index $i \in [n]$ and an image f(x) find the i-th pre-image bit $x_i$. In contrast, in his seminal work, Rudich [Rud88] proved that completely unstructured objects like one-way functions cannot construct even worst-case hard instances by fully black-box constructions. Here a fully black-box construction essentially means that the non-deterministic verifiers only make black-box use of the OWF (or OWP in the previous example) and the reduction establishing the hardness is also black-box (in both the adversary and the OWF).

But what about more structured primitives such as public-key encryption, oblivious transfer, or even indistinguishability obfuscation. Indeed, IO (plus OWFs) has-been shown to imply hardness in ${\textsf {PPAD}}$ and more generally in the class ${\textsf {TFNP}}$ of total search problems, which is often viewed as the search analog of ${\textsf {NP}} \cap {\textsf {coNP}}$ [MP91]. We will show, however, that fully black-box constructions do not give rise to a hard problem in ${\textsf {NP}} \cap {\textsf {coNP}}$ from OWFs (or even injective OWFs) and IO for circuits with OWF gates.

3.2 Fully Black-Box Constructions of Hardness in ${\textsf {NP}} \cap {\textsf {coNP}}$ from IO and IOWFs

We start by defining ${\textsf {NP}} \cap {\textsf {coNP}}$ relative to oracles [Rud88]. This, in particular, captures black-box constructions of such languages from cryptographic primitives, such as one-way functions in [Rud88] or indistinguishability obfuscation, which we will consider in this work.

Definition 3.1

( ${\mathsf {NP}} \cap {\mathsf {coNP}}$ relative to oracles ). Let $\mathfrak {S}$ be a family of oracles and let $V_1^{(\cdot )},V_0^{(\cdot )}$ be a pair of oracle-aided non-deterministic polynomial-time verifiers. We say that $V_1,V_0$ define a collection of languages in ${\mathsf {NP}} \cap {\mathsf {coNP}}$ relative to $\mathfrak {S}$ if for any $\varGamma \in \mathfrak {S}$, the machines $V_1^{\varGamma },V_0^{\varGamma }$ define a language $L^{\varGamma } \in {\mathsf {NP}} ^{\varGamma }\cap {\mathsf {coNP}} ^{\varGamma }$. That is

We now formally define the class of constructions and reductions ruled out. That is, fully black-box constructions of hard problems in ${\textsf {NP}} \cap {\textsf {coNP}}$ from injective one-way functions (IOWFs) and IO for IOWF-aided circuits. The definition is similar in spirit to those in [AS15, AS16] and in the Sect. 2, adapted to the context of ${\textsf {NP}} \cap {\textsf {coNP}}$ hardness.

Definition 3.2

A fully black-box construction of a hard ${\mathsf {NP}} \cap {\mathsf {coNP}}$ problem $L$ from IOWFs and IO for the class $\mathcal {C}$ of circuits with IOWF-gates is given by two oracle aided poly-time machines $(V_0,V_1)$ and a probabilistic oracle-aided reduction $\mathcal {R}$ that satisfy:

• 1. Structure: Let $\mathfrak {S}$ be the family of all oracles $({{f}},{{i\mathcal {O}}})$ such that ${{f}}$ is injective and ${{i\mathcal {O}}}$ is a function such that ${\widehat{C}}^{{f}}\equiv C^{{f}}$ for any $C^{(\cdot )}\in \mathcal {C}$, r, and ${\widehat{C}}^{(\cdot )}\,:=\,{{i\mathcal {O}}}(C,r)$. Then $(V_0,V_1)$ define a language $L^{{{f}},{{i\mathcal {O}}}}\in {\mathsf {NP}}^{{{f}},{{i\mathcal {O}}}} \cap {\mathsf {coNP}}^{{{f}},{{i\mathcal {O}}}}$ relative to any oracle $({{f}},{{i\mathcal {O}}}) \in \mathfrak {S}$ (as per Definition 3.1).

• 2. Black-box security proof: There exist functions $q_\mathcal {R}(\cdot ), \varepsilon _\mathcal {R}(\cdot )$ such that the following holds. Let $({{f}},{{i\mathcal {O}}})$ be any distribution supported on the family $\mathfrak {S}$ defined above. Then for any probabilistic oracle-aided $\mathcal {A}$ that decides $L^{{{f}},{{i\mathcal {O}}}}$ in the worst-case, namely, for all $n\in \mathbb {N}$

  

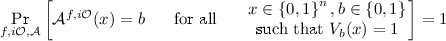
  the reduction breaks either ${{f}}$ or ${{i\mathcal {O}}}$, namely, for infinitely many $n\in \mathbb {N}$ either

  

  or

  $$\begin{aligned}&\left| \Pr \left[ {\mathsf {Exp}}^{\mathsf {iO}}_{({{f}},{{i\mathcal {O}}}), {{i\mathcal {O}}}, \mathcal {C},\mathcal {R}^{\mathcal {A}}}(n) = 1\right] -\frac{1}{2}\right| \ge \varepsilon _\mathcal {R}(n), \end{aligned}$$

  where in both $\mathcal {R}$ makes at most $q_\mathcal {R}(n)$ queries to any of its oracles $(\mathcal {A},{{f}},{{i\mathcal {O}}})$, and for any query x made to $\mathcal {A}$, the non-deterministic verifiers $V_0^{{{f}},{{i\mathcal {O}}}}(x),V_1^{{{f}},{{i\mathcal {O}}}}(x)$ make at most $q_\mathcal {R}(n)$ queries to their oracles (for any non-deterministic choice of a witness w). The random variable ${\mathsf {Exp}}^{\mathsf {iO}}_{({{f}},{{i\mathcal {O}}}), {{i\mathcal {O}}}, \mathcal {C},\mathcal {R}^{\mathcal {A}}}(n)$ represents the reductions winning probability in the IO security game relative to $({{f}},{{i\mathcal {O}}})$.

Remark about Correct Structure. We note that here we explicitly do put a correctness requirement, which we refer to as structure; namely, that the construction yields a language in ${\textsf {NP}} \cap {\textsf {coNP}}$ for any implementation of OWPs and IO. This is different from the setting from Definition 2.2 where we considered promise problems and allowed the construction not to satisfy the promise occasionally.

Concretely, we require that $V_0,V_1$ give a language in ${\textsf {NP}} \cap {\textsf {coNP}}$ for every oracle implementing IOWFs and IO. This follows the modeling of [BI87],¹¹ and aligns with how we usually think about correctness of black-box constructions of cryptographic primitives. For instance, the construction of public-key encryption from trapdoor permutations is promised to be correct, for all oracles implementing the trapdoor permutation. Similarly, the construction of hard ${\textsf {NP}} \cap {\textsf {coNP}}$ languages from one-way permutations, give an ${\textsf {NP}} \cap {\textsf {coNP}}$ language for any oracle implementing a permutation.

We also note that as in Definition 2.2, our definition addresses worst-case hardness, which makes our impossibility result stronger. See further discussion after Definition 2.2.

Ruling out Fully Black-Box Constructions: A Road Map. Our main result in this section is that fully black-box constructions of a hard ${\textsf {NP}} \cap {\textsf {coNP}}$ problem from IO and IOWFs do not exist. Furthermore, this holds even if the latter primitives are exponentially secure.

Theorem 3.3

Any fully black-box construction of an ${\mathsf {NP}} \cap {\mathsf {coNP}}$ problem $L$ from IOWFs and IO for circuits with IOWF gates has an exponential security loss:

$$\max (q_{\mathcal {R}}(n), \varepsilon _{\mathcal {R}}^{-1}(n)) \ge \varOmega (2^{n/6})$$

The proof of the theorem follows a similar methodology to the proof of Theorem 2.3. We exhibit two (distributions on) oracles $(\varPsi ,\mathsf {Decide}^{\varPsi })$, where $\varPsi$ realizes IOWFs and IO for circuits with IOWF gates, and $\mathsf {Decide}^{\varPsi }$ that decides $L^{\varPsi } \in {\mathsf {NP}}^{\varPsi } \cap {\mathsf {coNP}}^{\varPsi }$ in the worst case. We then show that the primitives realized by $\varPsi$ are (exponentially) secure even in the presence of $\mathsf {Decide}^{\varPsi }$. Then viewing $\mathsf {Decide}$ as a worst-case decider $\mathcal {A}$ (as per Definition 3.2) directly implies Theorem 3.3, ruling out fully black-box constructions with a subexponential security loss.

We defer the formal treatment to the full version.

4 Collision-Resistance from IO and SZK-Hardness

Asharov and Segev [AS15] showed that collision-resistant hashing cannot be constructed from (even subexponentially hard) indistinguishability obfuscation (IO) and one-way permutations (OWPs) relying on common IO techniques. Slightly more accurately, they rule out fully black-box constructions where (as in previous sections) IO is defined with respect to circuits with OWP oracle gates. In this section, we show that, assuming IO and a strong form of ${\textsf {SZK}}$-hardness, there is indeed a construction of collision-resistant hashing (CRH).

The High-Level Idea Behind the Construction. The starting point for our construction is the work of Ishai et al. [IKO05] that shows how to construct collision-resistant hash functions from commitments that are additively homomorphic (for simplicity, say over $\mathbb {F}_2)$. The idea is simple: we can hash $\ell$ bits to m bits, where m is the size of a single bit commitment and $\ell$ can be arbitrarily longer, as follows. The hash key is a commitment $\gamma :=(\mathsf {com}(\beta _1),\dots ,\mathsf {com}(\beta _\ell ))$ to a random vector $\beta \in \mathbb {F}_2^{\ell }$, and hashing $x\in \mathbb {F}_2^\ell$, is done by homomorphically computing a commitment to the inner product $\mathsf{CRH}_{\gamma }(x) = \mathsf {com}(\langle \beta ,x\rangle )$.

This idea can, in fact, be abstracted to work with any commitment scheme wherein given a commitment $\mathsf {com}(\beta )$ for a random key for a 2-universal hash allows to homomorphically compute a commitment $\mathsf {com}(\mathsf{2UH}_{\beta }(x))$ to the hash at any point x, so that the resulting commitment is compact in the sense that it depends only on the size of $\mathsf{2UH}_{\beta }(x)$ and not on the size of x. Intuitively, the reason this works is that any collision in $\mathsf{CRH}_{\gamma }$ implies a collision in the underlying 2-universal hash $\mathsf{2UH}_{\beta }$, which leaks information about the hash key $\beta$ (concretely, any fixed $x,x'$ form a collision in a random hash function with small probability) thereby violating the hiding of the commitment.

At a high-level, we aim to mimic the above construction based on obfuscation. As a key for the collision-resistant hash we can obfuscate a program $\varPi _{\beta }$ associated with a secret hash key $\beta$ that given x outputs a commitment $\mathsf {com}(\mathsf{2UH}_{\beta }(x))$, where the commitment is derandomized using a PRF. The obfuscation $i\mathcal {O}(\varPi _{\beta })$ can be thought of as the commitment to $\beta$, and evaluating this program at x, corresponds to homomorphic evaluation. Despite the clear intuition behind this construction, it is not clear how to prove its security based on IO. In fact, by [AS15], it cannot be proven based on a black-box reduction as long as plain statistically-binding commitments are used, as these can be constructed from OWPs in a fully black-box manner.

We show, however, that relying on a relaxed notion of perfectly-hiding commitments, as well as subexponential hardness of IO and puncturable PRFs, the construction can be proven secure. The perfect hiding of the commitment is leveraged in a probabilistic IO argument [CLTV15] that involves a number of hybrids larger than the overall number of commitments. We then observe that these relaxed commitments follow from appropriate average-case hardness of ${\textsf {SZK}}$.¹²