1 Introduction

Side-channel analysis attacks (SCA) [41] are cheap and scalable methods to extract secrets, such as cryptographic keys or passwords, from embedded electronic devices. They exploit unintended signals (such as the instantaneous power consumption [42] or the electromagnetic radiation [24]) stemming from a cryptographic implementation. In the last twenty years, plenty of countermeasures to mitigate the impact of side-channel information have been developed. Masking [15, 26] is an established solution that stands out as a provably secure yet practically useful countermeasure.

Fault analysis (FA) is another relevant attack vector for embedded cryptography. The basic principle is to disturb the cryptographic computation somehow (for example, by under-powering the cryptographic device, or by careful illumination of certain areas in the silicon die). The result of a faulty computation can reveal a wealth of secret information: in the case of RSA or AES, a single faulty ciphertext pair makes key recovery possible [10, 48]. Countermeasures are essentially based on adding some redundancy to the computation (in space or time). In contrast to masking, the countermeasures for fault analysis are mostly heuristic and lack a formal background.

However, there is a tension between side-channel countermeasures and fault analysis countermeasures. On the one hand, fault analysis countermeasures require redundancy, which can give out more leakage information to an adversary. On the other hand, a device that implements first-order masking offers an adversary double the attack surface to insert a fault in the computation. A duality relation between SCA and FA was pointed out in [23]. There is clearly a need for a combined countermeasure that tackles both problems simultaneously.

In this work we introduce a new attack model to capture this combined attack surface which we call the tile-probe-and-fault model. This model naturally extends the wire-probe model of [34]. In the wire-probe model individual wires of a circuit may be targetted for probing. The goal is then to protect against a certain fixed set of wire-probes. In our model, inspired by modern processor designs, we allow whole areas (or tiles) to be probed, and in addition we add the possibility of the attacker inducing faults on such tiles.

Protection against attacks in the wire-probe model is usually done via masking; which is in many cases the extension of ideas from passively secure secret sharing based Multi-Party Computation (MPC) to the side-channel domain. It is then natural to look at actively secure MPC protocols for the extension to fault attacks. The most successful modern actively secure MPC protocols are in the SPDZ family [20]. These use a pre-processing or preparation phase to produce so called Beaver triples, named after Beaver [6]. These auxiliary data values, which will be explained later, are prepared either before a computation, or in a just-in-time manner, so as to enable an efficient protocol to be executed. This use of prepared Beaver triples also explains, partially, the naming of our system, CAPA (a Combined countermeasure Against Physical Attacks), since Capa is also the beaver spirit in Lakota mythology. In this mythology, Capa is the lord of domesticity, labour and preparation.

1.1 Previous Work

Fault Attack Models and Countermeasures: Faults models typically describe the characterization of an attacker’s ability. That is, the fault model is constructed as a combination of the following: the precision of the fault location and time, the number of affected bits which highly depends on the architecture, the effect of the fault (flip/set/reset/random) and its duration (transient/permanent). Moreover, the fault can target the clock or power line, storage units, combinational or control logic.

When it comes to countermeasures, one distinguishes between protection of the algorithm on the one hand and protection of the device itself by using, for example, active or passive shields on the other. No countermeasure provides perfect security at a finite cost; it is the designer’s responsibility to strive for a balance between high-level (algorithmic) countermeasures and low-level ones that work at the circuit level and complement each other. In this paper, we discuss the former.

One algorithmic technique is to replicate the calculation m times in either time or space and only complete if all executions return the same result [54]. This countermeasure has the important caveat that there are conceptually simple attacks, such as m identical fault injections in each execution, that break the implementation with probability one. However, it should be stated that these attacks are not trivial to mount in practice when the redundancy is in space.

A second method is to use an error correcting or detecting code [8, 12, 13, 32, 35,36,37,38,39, 46]. This means one performs all calculations on both data and checksum. A drawback is that error correcting/detecting codes only work in environments in which errors are randomly generated, as opposed to maliciously generated. Thus, a skilled attacker may be able to carefully craft a fault that results in a valid codeword and is thus not detected. A detailed cost comparison between error detection codes and doubling is given in [44].

Another approach is that of infective computation [25, 43], where any fault injected will affect the ciphertext in a way that no secret information can be extracted from it. This method ensures the ciphertext can always be returned without the need for integrity checks. While infective methods are very efficient, the schemes proposed so far have all been broken [5].

Side-Channel Attack Models and Countermeasures: A side-channel adversary typically uses the noisy leakage model [55], where side-channel analysis (SCA) attacks are bounded by the statistical moment of the attack due to a limited number of traces and noisy leakages. Given enough noise and an independent leakage assumption of each wire, this model, when limited to the \(t^\text {th}\)-order statistical moment, is shown to be comparable to the t-probing model introduced in [34], where an attacker is allowed to probe, receive and combine the noiseless information about t wires within a time period [21]. Finally, it has been shown in [4] that a (semi-)parallel implementation is secure in the \(t^\text {th}\)-order bounded moment model if its complete serialization is secure at the t-probing model.

While the countermeasures against fault attacks are limited to resist only a small subset of the real-world adversaries and attack models, protection against side-channel attacks stands on much more rigorous grounds and generally scales well with the attacker’s powers. A traditional solution is to use masking schemes [9, 29, 34, 51, 56, 58, 59] to implement a function in a manner in which higher-order SCA is needed to extract any secret information, i.e. the attacker must exploit the joint leakage of several intermediate values. Masking schemes are analogues of the passively secure threshold MPC protocols based on secret sharing. One can thus justify their defence by appealing to the standard MPC literature. In MPC, a number of parties can evaluate a function on shared data, even in the presence of adversaries amongst the computing parties. The maximum number of dishonest parties which can be tolerated is called the threshold. In an embedded scenario, the basic idea is that different parts of a chip simulate the parties in an MPC protocol.

Combining Faults and Side-Channels Models and Countermeasures. The importance of combined countermeasures becomes more apparent as attacks such as [2] show the feasibility of combined attacks. Being a relatively new threat, combined adversarial models lack a joint description and are typically limited to the combination of a certain side-channel model and a fault model independently.

One possible countermeasure against combined attacks is found in leakage resilient schemes [45], although none of these constructions provide provable security against FA. Typical leakage resilient schemes rely on a relatively simple and easy to protect key derivation function in order to update the key that is used by the cryptographic algorithm within short periods. That is, a leakage resilient scheme acts as a specific “mode of operation”. Thus, it cannot be a drop-in replacement for a standard primitive such as the AES block cipher. The aforementioned period can be as short as one encryption per key in order to eliminate fault attacks completely. However, the synchronization burden this countermeasure brings, makes it difficult to integrate with deployed protocols.

There are a couple of alternative countermeasures proposed for embedded systems in recent years. In private circuits II [16, 33], the authors use redundancy on top of a circuit that already resists SCA (private circuits I [34]) to add protection against FA. In ParTI [62], threshold implementations (TI) are combined with concurrent error detection techniques. ParTI naturally inherits the drawbacks of using an error correction/detection code. Moreover, the detectable faults are limited in hamming weight due to the choice of the code. Finally, in [63], infective computation is combined with error-preserving computation to obtain a side-channel and fault resistant scheme. However, combined attacks are not taken into account.

Given the above introduction, it is clear that both combined attack models and countermeasures are not mature enough to cover a significant part of the attack surface.

Actively Secure MPC. Modern MPC protocols obtain active security, i.e. security against malicious parties which can actively deviate from the protocol. By mapping such protocols to the on-chip side-channel countermeasures, we would be able to protect against an eavesdropping adversary that inserts faults into a subset of the simulated parties. An example of a practical attack that fits this model is the combined attack of Amiel et al. [2]. We place defences against faults on the same theoretical basis as defences against side-channels.

To obtain maliciously secure MPC protocols in the secret-sharing model, there are a number of approaches. The traditional approach is to use Verifiable Secret Sharing (VSS), which works in the information theoretic model and requires that strictly less than n / 3 parties can be corrupt. The modern approach, adopted by protocols such as BODZ, SPDZ, Tiny-OT, MASCOT etc. [7, 20, 40, 50], is to work in a full threshold setting (i.e. all but one party can be corrupted) and attach information theoretic MACs to each data item. This approach turns out to be very efficient in the MPC setting, apart from its usage of public-key primitives. The computational efficiency of the use of information theoretic MACs and the active adversarial model of SPDZ lead us to adopt this philosophy.

1.2 Our Contributions

Our contributions are threefold. We first introduce the tile-probe-and-fault model, a new adversary model for physical attacks on embedded systems. We then use the analogy between masking and MPC to provide a methodology, which we call CAPA, to protect against such a tile-probe-and-fault attacker. Finally, we illustrate that the CAPA methodology can be prototyped by describing specific instantiations of the CAPA methodology, and our experimental results.

Fig. 1.
figure 1

Partition of the integrated circuit area into tiles, implementing MPC “parties”

Full size image

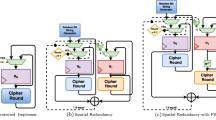
Tile-probe-and-fault model. We introduce a new adversary model that expands on the wire-probe model and brings it closer to real-world processor designs. Our model is set in an architecture that mimics the actively secure MPC setting that inspires our countermeasures (see Fig. 1). Instead of individual wires at the foundation of the model, we visualize a separation of the chip (integrated circuit) into areas or tiles, consisting of not only many wires, but also complete blocks of combinational and sequential logic. Such tiled designs are inherent in many modern processor architectures, where the tiles correspond to “cores” and the wires correspond to the on-chip interconnect. This can easily be related to a standard MPC architecture where each tile behaves like a separate party. The main difference between our architecture and the MPC setting is that in the latter, parties are assumed to be connected by a complete network of authenticated channels. In our architecture, we know exactly how the wires are connected in the circuit.

The tile architecture satisfies the independent leakage assumption [21] amongst tiles. That is, leakage is local and thus observing the behaviour of a tile by means of probing, faulting or observing its side-channel leakage, does not give unintended information about another tile through, for example, coupling.

As the name implies, the adversary in our model exploits side-channels and introduces faults. We stress that our goal is to detect faults as opposed to tolerate or correct them. That is, if an adversary interjects a fault, we want our system to abort without revealing any of the underlying secrets.

CAPA Methodology. We introduce CAPA, a countermeasure against the tile-probe-and-fault-attacker, which is suitable for implementation in both hardware and software. CAPA inherits theoretical aspects of the MPC protocol SPDZ [20] by similarly computing on shared values, along with corresponding shared MAC tags. The former prevents the adversary from learning sensitive values, while the latter allows for detection of any faults introduced. Moreover, having originated from the MPC protocol SPDZ, CAPA is the first countermeasure with provable security against combined attacks. The methodology can be scaled to achieve an arbitrary fault detection probability and is suitable for implementation in both hardware and software.

Experimental Results. We provide examples of CAPA designs in hardware of the KATAN and AES block ciphers as well as a software bitsliced implementation of the AES S-box. Our designs show that our methodology is feasible to implement, and in addition our attack experiments confirm our theoretical claims. For example, we implemented a second-order secure hardware implementation of KATAN onto a Spartan-6 FPGA and perform a non-specific leakage detection test, which does not show evidence of first- or second-order leakage with up to 100 million traces. Furthermore, we deploy a second-order secure software based CAPA implementation of the AES S-box on an ARM Cortex-M4 and take electromagnetic measurements; for this implementation neither first-nor second-order leakage is detected with up to 200 000 traces. Using toy parameters, we verify our claimed fault detection probability for the AES S-box software implementation. It should be noted that our experimental implementations are to be considered only proof-of-concept; they are currently too expensive to be used in practice. But the designs demonstrate that the overall methodology can provide significant side-channel and fault protection, and they provide a benchmark against which future improvements can be measured.

2 The Tile-Probe-and-Fault Model

The purpose of this section is to introduce a new adversarial model in which our security guarantees are based. This model is strictly more powerful than the traditional DPA or DFA models.

Tile Architecture. Consider a partition of the chip in a number of tiles \(\mathcal {T}_i\), with wires running between each pair of tiles as shown in Fig. 1. We call the set of all tiles \(\mathcal {T}\). Each tile \(\mathcal {T}_i \in \mathcal {T}\) possesses its own combinational logic, control logic (or program code) and pseudo-random number generator needed for the calculations of one share. In the abstract setting, we consider each tile as the set composed of all input and intermediate values on the wires and memory elements of those blocks. A probe-and-fault attacker may obtain, for a given subset of tiles, all the internal information at given time intervals on this set of tiles. He may also inject faults (known or random) into each tile in this set.

In our model, each sensitive variable is split into d shares through secret sharing. Without loss of generality, we use Boolean sharing in this paper.

We define each tile such that it stores and manipulates at most one share of each intermediate variable. Any wire running from one tile to another carries only blinded versions of a sensitive variables’ share used by \(\mathcal {T}_i\). We make minimal assumptions on the security of these wires. Instead, we include all the information on the unidirectional wires in Fig. 1 in the tile on the receiving and not the sending end. We thus assume only one tile is affected by an integrity failure of a wire. We assume that shared calculations are performed in parallel without loss of generalization. The redundancy of intermediate variables and logic makes the tiles completely independent apart from the communication through wires.

Probes. Throughout this work, we assume a powerful \(d_p\)-probing adversary where we give an attacker information about all intermediate values possessed by \(d_p\) specified tiles, i.e. \(\cup _{i \in {i_1,\ldots ,i_{d_p}}} \mathcal {T}_i\). The attacker obtains all the intermediate values on the tile (such as internal wire and register values) with probability one and obtains these values from the start of the computation until the end. Note that this is stronger than both the standard t-probing adversary which gives access to only t intermediate values within a certain amount of time [34] and \(\epsilon \)-probing adversary where the information about t intermediate values is gained with certain probability. In our \(d_p\)-probing model, the adversary gets information from n intermediate values from \(d_p\) tiles where \(n \gg d_p\). Therefore, our \(d_p\)-probing model is more generic and covers realistic scenarios including an attacker with a limited number of EM probes which enable observation of multiple intermediate values simultaneously within arbitrarily close proximity on the chip.

Faults. We also consider two types of fault models. Firstly, a \(d_f\)-faulting adversary which can induce chosen-value faults in any number of intermediate bits/values within \(d_f\) tiles, i.e. from the set \(\cup _{i \in {i_1,\ldots ,i_{d_f}}} \mathcal {T}_i\). These faults can have the nature of either flipping the intermediate values with a pre-calculated (adversarially chosen) offset or setting the intermediate values to a chosen fixed value. In particular, the faults are not limited in hamming weight. One can relate this type of faults with, for example, very accurate laser injections.

Secondly, we consider an \(\epsilon \)-faulting adversary which is able to insert a random-value fault in any variable belonging to any party. This is a somehow new MPC model, and essentially means that all parties are randomly corrupted. The \(\epsilon \)-adversary may inject the random-value fault according to some distribution (for example, flip each bit with certain probability), but he cannot set all intermediates to a chosen fixed value. This adversary is different from the \(d_f\)-faulting adversary. One can relate the \(\epsilon \)-faulting adversary to a certain class of non-localised EM attacks.

Time Periods. We assume a notion of time periods; where the period length is at least one clock cycle. We require that a \(d_f\)-fault to an adversarially chosen value cannot be preceded by a probe within the same time period. Thus adversarial faults can only depend on values from previous time periods. This time restriction is justified by practical experimental constraints; where the time period is naturally upper bounded by the time it takes to set up such a specific laser injection.

Adversarial Models. Given the aforementioned definitions, we consider on the one hand an active adversary \(\mathscr {A}_1\) with both \(d_p\)-probing and \(d_f\)-faulting capabilities simultaneously. We define \(\mathcal {P}_1\) the set of up to \(d_p\) tiles that can be probed and \(\mathcal {F}_1\) the set of up to \(d_f\) tiles that can be faulted by \(\mathscr {A}_1\). Since each tile potentially sees a different share of a variable and we use a d-sharing for each variable, we constrain the attack surface (the sets of adversarially probed and potentially modified tiles) as follows:

$$\begin{aligned} ( \mathcal {F}_1 \cup \mathcal {P}_1 ) \subseteq \cup _{j=1}^{d-1} \mathcal {T}_{i_j} \end{aligned}$$

The constraint implies that at least one share remains unaccessed/honest and thus \(|\mathcal {F}_1 \cup \mathcal {P}_1| \le d-1\). Within those \(d-1\) tiles, the adversary can probe and fault arbitrarily many wires, including the wires arriving at each tile. The adversary’s \(d_f\)-faulting capabilities are limited in time by our definition of time periods, which implies that any \(d_f\)-fault cannot be preceded by another probe within the same time period.

We also consider an active adversary \(\mathscr {A}_2\) that has \(d_p\)-probing and \(\epsilon \)-faulting capabilities simultaneously. In this case, the constraint on the set of probed tiles \(\mathcal {P}_2\) remains the same:

$$\begin{aligned} \mathcal {P}_2 \subseteq \cup _{j=1}^{d-1} \mathcal {T}_{i_j} \end{aligned}$$

but the set of faulted tiles is no longer constrained:

$$\begin{aligned} \mathcal {F}_2 \subseteq \mathcal {T} \end{aligned}$$

Moreover, as \(\epsilon \)-faults do not require the same set-up time as \(d_f\)-faults, they are not limited in time. Note that, \(\epsilon \)-faults do not correspond to a standard adversary model in the MPC literature; thus this part of our model is very much an aspect of our side-channel and fault analysis focus. A rough equivalent model in the MPC literature would be for an honest-but-curious adversary who is able to replace the share or MAC values of honest players with values selected from a given random distribution. Whilst such an attack makes sense in the hardware model we consider, in the traditional MPC literature this model is of no interest due to the supposed isolated nature of computing parties.

As our constructions are based on MPC protocols which are statically secure we make the same assumptions in our tile-probe-and-fault model, i.e. the selection of tiles attacked must be fixed beforehand and cannot depend on information gathered during computation. This model reflects realistic attackers since it is infeasible to move a probe or a laser during a computation with today’s resources. We thus assume that both adversaries \(\mathscr {A}_1\) and \(\mathscr {A}_2\) are static.

3 The CAPA Design

The CAPA methodology consists of two stages. A preprocessing step generates auxiliary data, which is used to perform the actual cryptographic operation in the evaluation step. We first present some notation, then the building blocks for the main evaluation, and finally the preprocessing components.

Notation. Although generalization to any finite field holds, in this paper we work over a field \(\mathbb {F}_q\) with characteristic 2, for example \(GF(2^k)\) for a given k, as this is sufficient for application to most symmetric ciphers. We use \(\cdot \) and \(+\) to describe multiplication and addition in \(\mathbb {F}_q\) respectively. We use upper case letters for constants. The lower case letters x, y, z are reserved for the variables used only in the evaluation stage (e.g. sensitive variables) whereas \(a,b,c,\ldots \) represent auxiliary variables generated from randomness in the preprocessing stage. The kronecker delta function is denoted by \(\delta _{i,j}\). We use L(.) to denote an additively homomorphic function and \(A(.) = C + L(.)\) with C some constant.

Information Theoretic MAC Tags and the MAC Key \(\alpha \). We represent a value \(a \in \mathbb {F}_q\) (similarly \(x \in \mathbb {F}_q\)) as a pair \(\langle {\varvec{a}} \rangle = ({\varvec{a}}, \varvec{\tau }^{{\varvec{a}}})\) of data and tag shares in the masked domain. The data shares \({\varvec{a}} = (a_1, \ldots , a_d)\) satisfy \(\sum a_i = a\). For each \(a \in \mathbb {F}_q\), there exists a corresponding MAC tag \(\tau ^{a}\) computed as \(\tau ^{a} = \alpha \cdot a\), where \(\alpha \) is a MAC key, which is secret-shared amongst the tiles as \(\alpha = \sum \alpha _i\).

Analogously to the data, the MAC tag is shared \(\varvec{\tau }^{{\varvec{a}}} = (\tau ^{a}_1, \ldots , \tau ^{a}_d)\), such that it satisfies \(\sum \tau ^{a}_i = \tau ^{a}\), but the MAC key itself does not carry a tag. Depending on a security parameter m, there can be m independent MAC keys \(\alpha [j] \in \mathbb {F}_q\) for \(j \in \{1,\ldots ,m\}\). In that case, \(\alpha \) as well as \(\tau ^{a}\) are in \(\mathbb {F}_q^m\) and the tag shares satisfy \(\sum \tau ^{a}_i[j] = \tau ^{a}[j] = \alpha [j] \cdot a\), \(\forall j \in \{1,\ldots ,m\}\). Further we assume \(m=1\) unless otherwise mentioned.

3.1 Evaluation Stage

We let each tile \(\mathcal {T}_i\) hold the \(i^\text {th}\) share of each sensitive and auxiliary variable (\(x_i, \ldots \), \(a_i, \ldots \)) and the MAC key share \(\alpha _i\). We first describe operations that do not require communication between tiles.

Addition. To compute the addition \(({\varvec{z}}, \varvec{\tau }^{{\varvec{z}}})\) of \(({\varvec{x}}, \varvec{\tau }^{{\varvec{x}}})\) and \(({\varvec{y}}, \varvec{\tau }^{{\varvec{y}}})\), each tile performs local addition of their data shares \(z_i=x_i + y_i\) and their tag shares \(\tau ^{z}_{i} = \tau ^{x}_i + \tau ^{y}_i\). When one operand is public (for example, a cipher constant \(C \in \mathbb {F}_q\)), the sum can be computed locally as \(z_i = x_i + C \cdot \delta _{i,1}\) for value shares and \(\tau ^{z}_i = \tau ^{x}_i + C \cdot \alpha _i\) for tag shares.

Multiplication by a Public Constant. Given a public constant \(C \in \mathbb {F}_q\), the multiplication \(({\varvec{z}},\varvec{\tau }^{{\varvec{z}}})\) of \(({\varvec{x}},\varvec{\tau }^{{\varvec{x}}})\) and C is obtained locally by setting \(z_i = C \cdot x_i\) and \(\tau ^{z}_i = C \cdot \tau ^{x}_i\).

The following operations, on the other hand, require auxiliary data generated in a preprocessing stage and also communication between the tiles.

Multiplication. Multiplication of \(({\varvec{x}}, \varvec{\tau }^{{\varvec{x}}})\) and \(({\varvec{y}}, \varvec{\tau }^{{\varvec{y}}})\) requires as auxiliary data a Beaver triple \((\langle {\varvec{a}} \rangle , \langle {\varvec{b}} \rangle , \langle {\varvec{c}} \rangle )\), which satisfies \(c=a \cdot b\), for random a and b. The multiplication itself is performed in four steps.

  • Step A. In the blinding step, each tile \(\mathcal {T}_i\) computes locally a randomized version of its share of the secret: \(\varepsilon _i = x_i + a_i\) and \(\eta _i = y_i + b_i\).

  • Step B. In the partial unmasking step, each tile \(\mathcal {T}_i\) broadcasts its own shares \(\varepsilon _i\) and \(\eta _i\) to other tiles, such that each tile can construct and store locally the values \(\varepsilon =\sum \varepsilon _i\) and \(\eta =\sum \eta _i\). The value \(\varepsilon \) (resp. \(\eta \)) is the partial unmasking of \((\varvec{\varepsilon }, \varvec{\tau }^{\varvec{\varepsilon }})\) (resp. \((\varvec{\eta }, {\varvec{\tau }^{\varvec{\eta }}})\)), i.e. the value \(\varepsilon \) (resp. \(\eta \)) is unmasked but its tag \({\varvec{\tau }^{\varvec{\varepsilon }}}\) (\({\varvec{\tau }^{\varvec{\eta }}}\)) remains shared. These values are blinded versions of the secrets x and y and can therefore be made public.

  • Step C. In the MAC-tag checking step, the tiles check whether the tags \({\varvec{\tau }^{\varvec{\varepsilon }}}\) (\({\varvec{\tau }^{\varvec{\eta }}}\)) are consistent with the public values \(\varepsilon \) and \(\eta \), using a method which we will explain later in this section.

  • Step D. In the Beaver computation step, each tile locally computes

    $$\begin{aligned} z_i&= c_i + \varepsilon \cdot b_i + \eta \cdot a_i + \varepsilon \cdot \eta \cdot \delta _{i,1}\\ \tau ^{z}_i&= \tau ^{c}_i + \varepsilon \cdot \tau ^{b}_i + \eta \cdot \tau ^{a}_i + \varepsilon \cdot \eta \cdot \alpha _i. \end{aligned}$$

It can be seen easily that the sharing \(({\varvec{z}}, \varvec{\tau }^{{\varvec{z}}})\) corresponds to \(z = x \cdot y\) unless faults occurred. Step B and C are the only steps that require communication among tiles. Step A and D are completely local. Note that to avoid leaking information on the sensitive data x and y, the shares \(\varepsilon _i\) and \(\eta _i\) must be synchronized using memory elements after step A, before being released to other tiles in step B. Moreover, we remark that step C does not require the result of step B and can thus be performed in parallel.

Squaring. Squaring is a linear operation in characteristic 2 fields. Hence, the output shares of a squaring operation can be computed locally using the input shares. However, obtaining the corresponding tag shares is non-trivial. To square \(({\varvec{x}},\varvec{\tau }^{{\varvec{x}}})\) into \(({\varvec{z}},\varvec{\tau }^{{\varvec{z}}})\), we therefore require an auxiliary tuple \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle )\) such that \(b=a^2\). The procedure to obtain \(({\varvec{z}},\varvec{\tau }^{{\varvec{z}}})\) mimics that of multiplication with some modifications: there is only one partially unmasked value \(\varepsilon = x+a\), whose tag needs to be checked, and each tile calculates \(z_i = b_i + \varepsilon ^2 \cdot \delta _{i,1}\) and \(\tau ^{z}_i = \tau ^{b}_i + \varepsilon ^2 \cdot \alpha _i\).

Following the same spirit, we can also perform the following operations.

Affine Transformation. Provided that we have access to a tuple \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle )\) such that \(b = A(a)\), we can compute \(({\varvec{z}},\varvec{\tau }^{{\varvec{z}}})\) satisfying \(z = A(x) = C + L(x)\), where L(x) is an additively homomorphic function over the finite field, by computing the output sharing as \(z_i = b_i + L(\varepsilon ) \cdot \delta _{i,1}\) and \(\tau ^{z}_i = \tau ^{b}_i + L(\varepsilon ) \cdot \alpha _i\).

Multiplication following Linear Transformations. The technique used for the above additively homomorphic operations can be generalized even further to compute \(z=L_1(x)\cdot L_2(y)\) in shared form, where \(L_1\) and \(L_2\) are additively homomorphic functions. A trivial methodology would require two tuples \((\langle {\varvec{a}}_{{\varvec{i}}} \rangle , \langle {\varvec{b}}_{{\varvec{i}}} \rangle )\) with \(b_i=L_i(a_i)\) for \(i \in \{1,2\}\), plus a standard Beaver triple (i.e. requiring seven pre-processed data items). We see that we can do the same operation with five pre-processed items \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle ,\langle {\varvec{d}} \rangle ,\langle {\varvec{e}} \rangle )\), such that \(c=L_1(a)\), \(d=L_2(b)\) and \(e=L_1(a) \cdot L_2(b)\). The tiles partially unmask \({\varvec{x}}+{\varvec{a}}\) (resp. \({\varvec{y}} + {\varvec{b}}\)) to obtain \(\varepsilon \) (resp. \(\eta \)) and verify them. Each tile computes its value share and tag share of z as \(z_i = e_i + L_1(\varepsilon ) \cdot d_i + L_2(\eta ) \cdot c_i + L_1(\varepsilon ) \cdot L_2(\eta ) \cdot \delta _{i,1}\) and \(\tau ^{z}_i = \tau ^{e}_i + L_1(\varepsilon ) \cdot \tau ^{d}_i + L_2(\eta ) \cdot \tau ^{c}_i + L_1(\varepsilon ) \cdot L_2(\eta ) \cdot \alpha _i\), respectively. We refer to \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle ,\langle {\varvec{d}} \rangle ,\langle {\varvec{e}} \rangle )\) as a quintuple.

Proof

figure a

Checking the MAC Tag of Partially Unmasked Values. Consider a public value \(\varepsilon = x + a\), calculated in the partial unmasking step of the Beaver multiplication operation. Recall that we obtain its MAC-tag shares as follows: \(\tau ^{\varepsilon }_i = \tau ^{a}_i + \tau ^{x}_i\). During the MAC-tag checking step of the Beaver operation, the authenticity of \(\tau ^{\varepsilon }\) corresponding to \(\varepsilon \) is tested. As \(\varepsilon \) is public, each tile can calculate and broadcast the value \(\varepsilon \cdot \alpha _i + \tau ^{\varepsilon }_i\). For a correct tag, we expect \(\sum \tau ^{\varepsilon }_i = \alpha \cdot \varepsilon \), thus each tile computes \(\sum ( \varepsilon \cdot \alpha _i + \tau ^{\varepsilon }_i )\) and proceeds if the result is zero. Recall that the broadcasting must be preceded by a synchronization of the shares.

Note on Unmasked Values/Calculations. There are several components in a cipher which do not need to be protected against SCA (i.e. masked), because their specific values are not sensitive. One prominent example is the control unit which decides what operations should be performed (e.g. the round counter). Other examples are constants such as the AES affine constant 0x63 or public values such as \(\varepsilon \) in a Beaver calculation and the difference \(\varepsilon \cdot \alpha + \tau ^{\varepsilon }\) during the MAC-tag checking phase.

While these public components are not sensitive in a SCA context, they can be targeted in a fault attack. It is therefore important to introduce some redundancy. Each tile should have its own control logic and keep a local copy of all public values to avoid single points of attack. The shares \(\varepsilon _i\) are distributed to all tiles so that \(\varepsilon \) can be unmasked by each tile separately and any subsequent computation performed on these public values is repeated by each tile. Finally, each tile also keeps its own copy of the abort status. This is in fact completely analogous to the MPC scenario.

3.2 Preprocessing Stage

The auxiliary data \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\ldots )\) required in the Beaver evaluations, is generated in a preprocessing stage. This preparation corresponds to the offline phase in SPDZ. However, CAPA’s preprocessing stage is lighter and does not require a public key calculation due to the differences in adversary model. As in SPDZ, this stage is completely independent from the sensitive data of the main evaluation. Below, we describe the generation of a Beaver triple used in multiplication. This can trivially be generalized to tuples and quintuples.

Auxiliary Data Generation. To generate a triple \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle )\) satisfying \(c=a\cdot b\), we draw random shares \({\varvec{a}}=(a_1, \ldots , a_d)\) and \({\varvec{b}} = (b_1, \ldots , b_d)\) and use a passively secure shared multiplier to compute \({\varvec{c}}\) s.t. \(c = a \cdot b\). We then use another such multiplication with the shared MAC key \(\varvec{\alpha }\) to generate tag shares \(\varvec{\tau }^{{\varvec{a}}}\), \(\varvec{\tau }^{{\varvec{b}}}\), \(\varvec{\tau }^{{\varvec{c}}}\). We note that the shares \(a_i,b_i\) are randomly generated by tile \(\mathcal {T}_i\). There are thus d separate PRNG’s on d distinct tiles.

Passively Secure Shared Multiplier. For a secure implementation of a shared multiplication, no subset of \(d-1\) tiles should have access to all shares of any variable. This concept, which is used in the context of secure implementations against SCA on hardware, is precisely called \(d-1^\text {th}\)-order non-completeness in [9, 52]. In the last decade, there has been significant improvement on passively secure shared multipliers that can be used in both hardware and software [9, 27, 29, 51, 56]. In principle, CAPA can use any such multiplier as long as the tile structure still holds.

A close inspection of existing multipliers show that they require the calculation of the cross products \(a_ib_j\). In order to make these multipliers compatible with the CAPA tile architecture, we define tiles \(\mathcal {T}_{i,j}\) which receive \(a_i\) from \(\mathcal {T}_{i}\) and \(b_j\) from \(\mathcal {T}_{j}\) where \(i \ne j\) in order to handle the pair \((a_i,b_j)\) to be used during tuple, triple and quintuple generation. This implies \(d(d-1)\) smaller tiles used only during auxiliary data generation in addition to d tiles used for both auxiliary data generation and evaluation. The output wires from \(\mathcal {T}_{i,j}\) are only connected to \(\mathcal {T}_{i}\) and carry randomized information.

The multipliers used in the preprocessing phase are only passively secure. We also ensure resistance against active adversaries because on the one hand, deterministic faults are limited to \(d-1\) tiles and on the other, because of a relation verification step, which is explained in the next section.

3.3 Relation Verification of Auxiliary Data

The information theoretic MAC tags provide security against faults induced in the evaluation stage. To detect faults in the preprocessing stage, we perform a relation verification of the auxiliary data. This relation verification step is done for each generated triple that is passed from the preprocessing to the evaluation stage and ensures that the triple is functionally correct (i.e. \(c = a\cdot b\)) by sacrificing another triple. That is, we take as input two triples \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle )\) and \((\langle {\varvec{d}} \rangle ,\langle {\varvec{e}} \rangle ,\langle {\varvec{f}} \rangle )\), that should satisfy the same relation, in this example \(c = a \cdot b\) and \(f = d \cdot e\). The following Beaver computation holds if and only if both relations are satisfied:

  • Draw a random \(r_1 \in \mathbb {F}_q\)

  • Use triple \((\langle {\varvec{d}} \rangle , \langle {\varvec{e}} \rangle , \langle {\varvec{f}} \rangle )\) to calculate the multiplication of \(r_1 \cdot \langle {\varvec{a}} \rangle \) and \(\langle {\varvec{b}} \rangle \) using a constant multiplication with \(r_1\), followed by the Beaver equation for multiplication described above. The result \(\langle {\tilde{{\varvec{c}}}} \rangle \) is a shared representation of \(\tilde{c} = r_1 \cdot a \cdot b\).

  • For each share i, calculate the difference with the shares and tags of \(r_1 \cdot c\): \(\varDelta _i = r_1 \cdot c_i + \tilde{c}_i\) and \(\tau ^{\varDelta }_i = r_1 \cdot \tau ^{c}_i + \tau ^{\tilde{c}}_i\).

  • Unmask the resulting differences \(\varDelta \) and \(\tau ^{\varDelta }\).

  • If a difference is nonzero, reject \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle )\) as a valid triple.

  • Pick another \(r_2 \in \mathbb {F}_q\) such that \(r_2 \ne r_1\) and repeat a second time.

Note that this relation verification ensures that the second triple is functionally correct too. However, it is burnt (or “sacrificed”) in this process in order to ensure that the first triple can be used securely further on. Note that this relation verification or “sacrificing” step is mandatory in each Beaver-like operation.

Why We Need Randomization. This sacrificing step involves two values \(r_1\) and \(r_2\). We present the following attack to illustrate why this randomization is needed. Again, we elaborate on triples, but the same can be said for tuples and quintuples. As the security does not rely on the secrecy of \(r_1\) and \(r_2\), we assume for simplicity that they are known to the attacker. We only stress that they are different: \(r_1 \ne r_2\).

Consider two triples \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle , \langle {\varvec{c}}^{\prime }\rangle )\) and \((\langle {\varvec{d}} \rangle ,\langle {\varvec{e}} \rangle , \langle {\varvec{f}}^{\prime }\rangle )\) at the input of the sacrificing stage. We assume that the adversary has introduced an additive difference into one share of \(c'\) and \(f'\) such that \(c' = a \cdot b + \varDelta _c\) and \(f' = d \cdot e + \varDelta _f\). This fault is injected before the MAC tag calculation, so that \(\tau ^{c'}\) and \(\tau ^{f'}\) are valid tags for the faulted values \(c'\) and \(f'\) respectively. In particular, this means we have \(\tau ^{c'} = \tau ^{c} + \alpha \cdot \varDelta _c\) and \(\tau ^{f'} = \tau ^{f} + \alpha \cdot \varDelta _f\).

The sacrificing step calculates the following four differences (for \(r_j = r_1\) and \(r_2\)) and only succeeds if all are zero.

$$\begin{aligned} \varDelta _j&= \sum _{i=1}^d\big ( r_j \cdot c'_i + f'_i + \varepsilon \cdot e_i + \eta \cdot d_i \big ) + \varepsilon \cdot \eta \\&= r_j \cdot \varDelta _c + \varDelta _f \overset{?}{=} 0 \\ \tau ^{\varDelta _j}&= \sum _{i=1}^d\big ( r_j \cdot \tau ^{c'}_i + \tau ^{f'}_i + \varepsilon \cdot \tau ^{e}_i + \eta \cdot \tau ^{d}_i + \varepsilon \cdot \eta \cdot \alpha _i \big ) \\&= r_j \cdot \alpha \cdot \varDelta _c + \alpha \cdot \varDelta _f \overset{?}{=} 0 \end{aligned}$$

Without randomization (i.e. \(r_1=r_2=1\)), the attacker only has to match the differences \(\varDelta _f = \varDelta _c\) to pass verification. With a random \(r_1\), the attacker can fix \(\varDelta _f = r_1 \cdot \varDelta _c\) to automatically force \(\varDelta _1\) and \(\tau ^{\varDelta _1}\) to zero. Even if he does not know \(r_1\), he has probability as high as \(2^{-k}\) to guess it correctly.

Only thanks to the repetition of the relation verification with \(r_2\), the adversary is detected with a probability \(1-2^{-km}\). Assuming he fixed \(\varDelta _f = r_1 \cdot \varDelta _c\), it is impossible to also achieve \(\varDelta _f = r_2 \cdot \varDelta _c\). Even if the attacker manages to force \(\varDelta _2\) to zero with an additive injection (since he knows all components \(r_2\), \(\varDelta _c\) and \(\varDelta _f\)), he cannot get rid of the difference \(\tau ^{\varDelta _2}=r_2 \cdot \alpha \cdot \varDelta _c + \alpha \cdot \varDelta _f\) without knowing the MAC key. Since \(\alpha \) remains secret, the attacker only has a success probability of \(2^{-km}\) to succeed.

4 Discussion

4.1 Security Claims

With both described adversaries \(\mathscr {A}_1\) and \(\mathscr {A}_2\), our design CAPA claims provable security against the following types of attacks as well as a combined attack of the two

  1. 1.

    Side-Channel Analysis (i.e. against \(d-1\) tile probing adversary).

  2. 2.

    Fault Attacks (i.e. an adversary introducing either known faults into \(d-1\) tiles or random faults everywhere).

Side-channel Analysis. One can check that no union of \(d-1\) tiles \(\cup _{j \in {j_1,\ldots ,j_{d-1}}} \mathcal {T}_j\) has all the shares of a sensitive value. Very briefly, we can reason to this \(d-1^\text {th}\)-order non-completeness as follows. All computations are local with the exception of the unmasking of public values such as \(\varepsilon \). However, the broadcasting of all shares of \(\varepsilon \) does not break non-completeness since \(\varepsilon = x + a\) is not sensitive itself but rather a blinded version of a sensitive value x, using a random a that is shared across all tiles. Unmasking the public value \(\varepsilon \) therefore gives each tile \(\mathcal {T}_i\) only one share \(\varepsilon + a_i\) of a new sharing of the secret x:

$$\begin{aligned} {\varvec{x}} = (a_1, \ldots , a_{i-1}, \varepsilon + a_i, a_{i+1}, \ldots , a_d) \end{aligned}$$

In this sharing, no union of \(d-1\) shares suffices to recover the secret. Our architecture thus provides non-completeness for all sensitive values. As a result, our d-share implementation is secure against \(d-1\)-probing attacks. Any number of probes following the adversaries’ restrictions leak no sensitive data. Our model is related to the wire-probe model, but with wires replaced by entire tiles. We can thus at least claim security against \(d-1^{\text {th}}\) order SCA.

Fault Attacks. A fault is only undetected if both value and MAC tag shares are modified such that they are consistent. Adversary \(\mathcal {A}_1\) can fault at most \(d_f < d\) tiles, which means he requires knowledge of the MAC key \(\alpha \in GF(2^{km})\) to forge a valid tag for a faulty value. Since \(\alpha \) is secret, his best option is to guess the MAC key. This guess is correct with probability \(2^{-km}\). Adversary \(\mathcal {A}_2\) has \(\epsilon \)-faulting abilities only and will therefore only avoid detection if the induced faults in value and tag shares happen to be consistent. This is the case with probability \(2^{-km}\). We can therefore claim an error detection probability (EDP) of \(1-\frac{1}{2^{km}}\). The EDP does not depend on the number of faulty bits (or the hamming weight of the injected fault).

Combined Attacks. In a combined attack, an adversary with \(d_f\)-faulting capabilities can mount an attack where he uses the knowledge obtained from probing some tiles \(\in \mathcal {P}_1\) to carefully forge the faults. In SPDZ, commitments are used to avoid the so called “rushing adversary”. CAPA does not need commitments as the timing limitation on \(\mathscr {A}_1\) adversary ensures a \(d_f\)-fault cannot be preceded by a probe in the same clock cycle. As a result, we inherit the security claims of SPDZ and the claimed EDP is not affected by probing or SCA. Also, the injection of a fault in CAPA does not change the side-channel security. Performing a side-channel attack on a perturbed execution does not reveal any additional information because the Beaver operations do not allow injected faults to propagate through a calculation into a difference that depends on sensitive information. We can claim this security, because of the aspects inherited from MPC. CAPA is essentially secure against a very powerful adversary that has complete control (hence combined attacks) over all but one of the tiles.

What Does Our MAC Security Mean? We stress that CAPA provides significantly higher security than existing approaches against faults. An adversary that injects errors in up to \(d_f\) tiles cannot succeed with more than the claimed detection probability. This means that our design can stand \(d^{\prime }_f \gg d_f\) shots if they affect at most \(d_f\) tiles. This is the case even if those \(d_f\) tiles leak their entire state; hence our resistance against combined attacks. The underlying reason for this is that to forge values, an attacker needs to know the MAC key, but since this is also shared, the attacker does not gain any information on the MAC key and their best strategy is to insert a random fault, which is detected with probability \(1-2^{-km}\). Moreover, our solution is incredibly scalable compared to for example error detection code solutions.

How Much Do Tags Leak? The tag shares \(\tau ^{a}_i\) form a Boolean masking of a variable \(\tau ^{a}\). This variable \(\tau ^{a}\) itself is an information theoretic MAC tag of the underlying value a and can be seen as a multiplicative share of a. We therefore require the MAC key to change for each execution. Hence MAC tag shares are a Boolean masking of a multiplicative share and are expected to leak very little information in comparison with the value shares themselves.

Forbidding the All-0s MAC Key. If the MAC key size mk is small, we should forbid the all-0 MAC key. This ensures that tags are injective: if an attacker changes a value share, he must change the tag share. We only pay with a slight decrease in the claimed detection probability. By excluding 1 of the \(2^{km}\) MAC key possibilities, we reduce the fault detection probability to \(1-2^{-\kappa }\), where \(\kappa = \log _2(2^{km}-1)\).

4.2 Attacks

The Glitch Power Supply or Clock Attack. The solution presented in this paper critically depends on the fact that there is no single point where an attacker can insert a fault that affects all d tiles deterministically. An attacker may try to glitch the chip clock line that is shared among all tiles. In this case, the attacker could try to carefully insert a glitch so that writing to the abort register is skipped or a test instruction is skipped. Since all tiles share the same clock, the attacker can bypass in this way the tag verification step. Similar comments apply, for example, to glitches in the power line. The bottom line is that one should design the hardware architecture accordingly, that is, deploy low-level circuit countermeasures that detect or avoid this attack vector.

Skipping Instructions. In software, when each tile is a separate processor (with its own program counter, program memory and RAM memory), skipping one instruction in up to \(d-1\) shares would be detected. The unaffected tiles will detect this misbehavior when checking partially unmasked values.

Safe Error Attack. We point out a specific attack that targets any countermeasure against a probing and faulting adversary. In a safe error attack [65], the attacker perturbs the implementation in a way that the output is only affected if a sensitive variable has a certain value. The attacker learns partial secret information by merely observing whether or not the computation succeeds (i.e. does not abort). Consider for example a shared multiplication of a variable x and a secret y and call the resulting product \(z = xy\). The adversary faults one of the inputs with an additive nonzero difference such that the multiplication is actually performed on \(x' = x + \varDelta \) instead of x. Such an additive fault can be achieved by affecting only one share/tile. The multiplication results in the faulty product \(z' = z + \varDelta \cdot y\). The injected fault has propagated into a difference that depends on sensitive data (y). As a result, the success or failure of any integrity check following this multiplication depends on y. In particular, if nothing happens (all checks pass), the attacker learns that y must be 0.

Among existing countermeasures against combined attacks, none provide protection against this kind of selective failure attack as they cannot detect the initial fault \(\varDelta \). The attacker can always target the wire running from the last integrity check on x to the multiplication with y. We believe CAPA is currently unique in preventing this type of attack. One can verify that the MAC-tag checking step in a Beaver operation successfully prevents \(\varDelta \) from propagating to the output. This integrity check only passes if all tiles have a correct copy of the public value \(\varepsilon \). Any faults injected after this check have a limited impact as the calculation finishes locally. That is, once the correct public values are established between the tiles, the shares of the multiplication output z are calculated without further communication among tiles. The adversary is thus unable to elicit a fault that depends on sensitive data.

PACA. We claim security against the passive and active combined attack (PACA) on masked AES described in [2] because CAPA does not output faulty ciphertexts. A second attack in this work uses another type of safe errors (or ineffective faults as they are called in this work) which are impossible to detect. The attacker fixes a specific wire to the value zero (this requires the \(d_f\)-faulting capability) and collects power traces of the executions that succeed. This means the attacker only collects traces of encryptions in which that specific wire/share was already zero. The key is then extracted using \(d-1^{\text {th}}\)-order SCA on the remaining \(d-1\) shares. This safe error attack however falls outside our model since the adversary gets access (either by fault or SCA) to all d shares and thus \((\mathcal {F}_1 \cup \mathcal {P}_1) = \mathcal {T}\).

Advanced Physical Attacks. In our description we are assuming that during the broadcast phase there are no “races” between tiles: by design, each tile sets its share to be broadcasted at clock cycle t and captures other tiles’ share in the same clock cycle t. We are implicitly assuming that tiles cannot do much work between these two events. If this assumption is violated (for example, using advanced circuit editing tools), a powerful adversary could bypass any verification. This is why in the original SPDZ protocol there are commitments prior to broadcasting operations; if this kind of attack is a concern one could adapt the same principles of commitments to CAPA. This is a very strong adversarial model that we consider out of scope for this paper.

4.3 Differences with SPDZ

Offline Phase. In SPDZ, the auxiliary data is generated using a somewhat homomorphic encryption scheme. The mapping onto a chip environment thus seems prohibitive due to the need for this expensive public-key machinery to obtain full threshold and the large storage required. We avoid this by generating the Beaver triples using passively secure shared multipliers. Furthermore, to avoid the large storage requirement, we produce the auxiliary data on the fly whenever required.

MAC Tag Checking. SPDZ delays the tag checking of public values until the very end of the encryption by using commitments. For this, each party keeps track of publicly opened values. This is to avoid a slowdown of the computation and because in the MPC setting, local memory is cheaper than communication costs. In an embedded scenario the situation is opposite so we check the opened values on the fly at the cost of additional dedicated circuit. In hardware, we “simulate” the broadcast channel by wiring between all tiles. Each tile keeps a local copy of those broadcasted values.

Adversary. Although MPC considers mainly the “synchronous” communication model, the SPDZ adversary model also includes the so-called “rushing” adversary, which first collects all inputs from the other parties and only then decides what to send in reply. In our embedded setting, as already pointed out, the “rushing” adversary is impossible. Due to the nature of the implementation, the computational environment and storage is very much restricted. On the other hand, communication channels are very efficient and can be assumed to be automatically synchronous with all tiles progressing in-step in the computation.

Table 1. Overview of the number of \(\mathbb {F}_q\) multiplications (.), \(\mathbb {F}_q\) additions (\(+\)) and linear operations in GF(2) (L(.)) required to calculate all building blocks with d shares and m tags
Full size table

4.4 Cost Analysis and Scalability

The computation as described in Sect. 3.1 scales nicely with the masking order d and the security parameter m. For any fixed number of shares d, the circuit area scales linearly in m (see for example Table 2). Storage increases with a factor \((m+1)d\) compared to a plain implementation. We note that our implementations run in almost the same amount of cycles as that of a plain implementation. There is almost no loss in throughput and only negligible in latency. In software as well, the timing scales linearly if tiles run in parallel (Table 1).

This efficiency does not come for free. The complexity is shifted to the preprocessing stage; indeed the generation of auxiliary triples is the most expensive part of the implementation. There is a trade-off to be made here between the online and offline complexity. The more auxiliary data we prepare “offline”, the more efficient the online computation.

Complexity for Passive Attacker Scenario. It is remarkable that if active attackers are ruled out, and only SCA is a concern, then the complexity of the principal computation is linear in d. This may seem like a significant improvement over previous masking schemes which have quadratic complexity on the security order [18, 34, 58]. However, this complexity is again pushed into the preprocessing stage. Nevertheless, this can be interesting especially for software implementations in platforms where a large amount of RAM is available to store the auxiliary data generated in Sect. 3.2. The same comments apply to FPGAs with plenty of BlockRAM.

Optimization of Preprocessing. It may be beneficial to store the output of the preprocessing stage Sect. 3.2 in a table for later usage. One could optimize this process by recycling auxiliary data (sample elements with replacement from the table). Of course, this would void the provable security claims; but if performed with care (with appropriate table shuffling and table elements refresh), this can give rise to an implementation that is secure in practice.

5 Proof-of-Concept

In this section we detail a proof-of-concept implementation of the CAPA methodology in both a hardware and a software environment. We emphasize specific concepts for hardware and software implementations and provide case studies of KATAN-32 [14] and AES [1], which cover operations in different fields, possibility of bitsliced implementations, specific timing and memory optimizations, and performance results.

5.1 Hardware Implementations

We now describe two case studies for applying CAPA in hardware. Our implementations are somewhat optimized for latency rather than area with d tiles spatially separated and operating in parallel, each with its own combinational and control logic and auxiliary data preparation module. These preparation modules are equipped with a passively secure shared multiplication with higher-order non-completeness. Literature provides us with a broad spectrum of multipliers to choose from [9, 27, 29, 51, 56]. In order to minimize the randomness requirement, our implementation uses the one from [29], hereafter referred to as DOM.

Library. For synthesis, we use Synopsis Design Compiler Version I-2013.12 using the NanGate 45 nm Open Cell library [49] for ease of future comparisons. We choose the compile option - exact_map to prevent optimization across tiles. The area results are provided in 2-input NAND-gate equivalents (GE).

Case Study: KATAN-32. KATAN-32 is a shift register based block cipher, which has a 80-bits key and processes 32-bit plaintext input. It is designed specifically for efficient hardware implementations and performs 254 cycles of four AND-XOR operations. Hence, its natural shared data representation is in the field \(\mathbb {F}_q = \mathrm {GF}(2)\), which makes the mapping into CAPA operations relatively straightforward. However, the small finite field means that we need to utilize a vectorized MAC-tag operation (\(m>1\)) to ensure a good probability of detecting errors. Our implementation is round based, as in [14] with three AND-XOR Beaver operations and one constant AND-XOR calculated in parallel. Each Beaver AND-XOR operation requires two cycles, and is implemented in a pipelined fashion such that the latency of the whole computation increases only by one clock cycle.

Implementation Cost. Tables 2 and 3 summarize the area of our KATAN implementations. Naturally, compared to a shared implementation without MAC tags, the state registers grow with a factor \(m+1\) as the MAC-key size increases. In the last columns, we extrapolate the area results for any m.

Table 2. Area (GE) of 2-share KATAN-32 implementations with m MAC keys \(\alpha [j] \in \mathbb {F}_q\)
Full size table
Table 3. Area (GE) of 3-share KATAN-32 implementations with m MAC keys \(\alpha [j] \in \mathbb {F}_q\)
Full size table

Each Beaver multiplication in \(\mathrm {GF}(2)\) requires one triple, and each triple needs 2d random bits for generating \({\varvec{a}}\) and \({\varvec{b}}\). A d-share DOM multiplication requires \(\left( {\begin{array}{c}d\\ 2\end{array}}\right) \) units of randomness. The construction of one triple requires \(1+3m\) masked multiplications: one to obtain the multiplication \({\varvec{c}}\) of \({\varvec{a}}\) and \({\varvec{b}}\); and 3m to obtain the m tags \(\varvec{\tau }^{{\varvec{a}}}\),\(\varvec{\tau }^{{\varvec{b}}}\) and \(\varvec{\tau }^{{\varvec{c}}}\). Due to the relation verification through the sacrificing of another triple, the randomness must be doubled. Hence, the total required number of random bits per round of KATAN is \(3 \cdot 2 \cdot (2d + (1+3m)\frac{d(d-1)}{2}) )\).

Fig. 2.
figure 2

Non-specific leakage detection on the first 31 rounds of first-order KATAN. Left column: PRNG off (24K traces). Right column: PRNG on (100M traces). Rows (top to bottom): exemplary power trace; first-order t-test; second-order t-test

Full size image
Fig. 3.
figure 3

Non-specific leakage detection on the first 31 rounds of second-order KATAN. Left column: PRNG off (24K traces). Right column: PRNG on (100M traces). Rows (top to bottom): exemplary power trace; first-order t-test; second-order t-test; third-order t-test

Full size image

Experimental Validation. The goal of the prior proof-of-concept implementation is to experimentally validate the protection against side-channel attacks offered by the CAPA methodology. We deploy a first- and second-order secure KATAN instance onto a Xilinx Spartan-6 FPGA. Our platform is a Sakura-G board specifically designed for side-channel evaluation with two FPGA’s to minimize platform noise: a control FPGA handles I/O with the host computer and supplies masked data to the crypto FPGA, which implements both the preprocessing and evaluation. The KATAN implementations use \(d=2\) (resp. \(d=3\)) shares and \(m=2\) MAC keys. The parameter \(m=2\) is insufficient in practice, but serves for this experiment since m has no influence on SCA security. The designs are clocked at 3 MHz and we sample power traces of 10 000 time samples each at 1 GS/s. Exemplary traces are shown in Fig. 2, top.

We perform a non-specific leakage detection test [17] following the methodology from [57, 61]. First, we test the designs without masks to verify that our setup is indeed sound and able to detect leakage. Then we switch on the PRNG and corroborate that the design does not leak with high confidence.

In Fig. 2, we show the results for the first-order secure design (\(d=2\)). In the left column, the PRNG is turned off, emulating an unmasked design. Indeed, we see clear leakage at first order, since the t-statistics cross the threshold 4.5. With the PRNG on (right column), no first-order leakage is detected with up to 100 million traces. As expected, we do see second-order leakage. Figure 3 exhibits the results for the second-order secure design (\(d=3\)). The left column shows clear leakage at first, second and third order when the PRNG is turned off. In the right column, we repeat the procedure with PRNG on and no univariate leakage is detected with up to 100 million traces.Footnote 1

Case Study: AES. There has been a great deal of work on MPC and masked implementations of the basic AES operations. We take what has now become the traditional approach and work in the field \(\mathrm {GF}(2^8)\) with \(m=1\) for AES, i.e. the MAC key, data and tag shares \(\alpha _i\), \(a_i\) and \(\tau ^{a}_i\) are \(\in \mathrm {GF}(2^8)\). The ShiftRows and MixColumns operations are linear in \(\mathrm {GF}(2^8)\), hence are straightforward. Here, we only describe the S-box calculation.

Design Choices. The AES S-box consists of an inversion in \(\mathrm {GF}(2^8)\), followed by an affine transformation over bits. We distinguish two methodologies for the S-box implementation: It is well known that the combination of the two operations can be expressed by the following polynomial in \(\mathrm {GF}(2^8)\) [19]:

$$\begin{aligned} \begin{aligned} {\text {S-box}}(x) =&\mathtt {0x63} + \mathtt {0x8F} \cdot x^{127} + \mathtt {0xB5} \cdot x^{191} + \mathtt {0x01} \cdot x^{223} + \mathtt {0xF4} \cdot x^{239} \\&+ \, \mathtt {0x25} \cdot x^{247} + \mathtt {0xF9} \cdot x^{251} + \mathtt {0x09} \cdot x^{253} + \mathtt {0x05} \cdot x^{254} \\ \end{aligned} \end{aligned}$$
(1)

This polynomial can be implemented using 6 squares and 7 multiplications in \(\mathrm {GF}(2^8)\) with a latency of 13 clock cyles. A second approach is to evaluate the inversion \(x \longrightarrow x^{254}\) using the following multiplication chain from [30]:

$$\begin{aligned} x^{254} = x^4 \cdot \Big ( \big ( ( x^5 )^5 \big )^5 \Big )^2 \end{aligned}$$

Since the AES affine transform A(x) is linear over \(\mathrm {GF}(2)\), we can then use the Beaver operation described in Sect. 3.1 to evaluate it in one cycle, using auxiliary affine tuples \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle )\) such that \(b=A(a)\). Initial estimations reveal the former method is more expensive than the latter, so we adopt the latter technique.

Multiplication Chain. Our implementation of the proposed multiplication chain uses two types of operations: \(x^5\) and \(x^4 \cdot y^2\), which can both be computed as described in Sect. 3.1 (Multiplication following Linear Transformations). Given an input \(\langle {\varvec{x}} \rangle \) and a triple \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle )\) such that \(b=a^4\) and \(c=a^5\), we calculate the CAPA exponentiation to the power five. Likewise, we perform the map \(x^4 \cdot y^2\) (with \(y=x^{125}\)) in one cycle, using quintuples \((\langle {\varvec{a}} \rangle ,\langle {\varvec{b}} \rangle ,\langle {\varvec{c}} \rangle ,\langle {\varvec{d}} \rangle ,\langle {\varvec{e}} \rangle )\) such that \(c=a^4\), \(d=b^2\) and \(e=c\cdot d = a^4 \cdot b^2\). As a result, an inversion in \(\mathrm {GF}(2^8)\) costs only 4 cycles, using 3 exponentiation triples and 1 quintuple. Combined with the affine stage, we obtain the S-box output in 5 cycles (see Fig. 4). This approach does not only optimize the number of cycles but also the amount of required randomness. The S-box is implemented as a five stage pipeline.

Fig. 4.
figure 4

AES S-box pipeline

Full size image

Implementation Cost. We use a serialized AES architecture, based on that in [28]. One round of the cipher requires 21 clock cycles, making the latency of one complete encryption 226 clock cycles. Since the unprotected serialised implementation of [47] also requires 226 cycles, the timing performance is very good.

Table 4 presents the area for the different blocks that make up our AES implementation. We can see a significant difference between the preprocessing and evaluation stages, i.e. the efficient calculation phase comes at the cost of expensive resource generation machinery.

Table 4. Areas for first- and second-order AES implementations with \(m=1\) in 2-NAND Gate Equivalents (GE)
Full size table

Table 5 summarizes the required number of random bytes for the generation of the triples/tuples for the AES S-box as a function of the number of MAC keys m and the number of shares d. Recall that the S-box needs three exponentiation triples, one quintuple and one affine tuple per cycle (doubled for the sacrificing). Each of these uses d initial bytes of randomness per input for the shares of a (and b). Furthermore, recall that each masked multiplication requires \(\left( {\begin{array}{c}d\\ 2\end{array}}\right) \) bytes or randomness. That is, for \(d=3\) and \(m=1\), we need 156 bytes of randomness per S-box evaluation.

Table 5. The number of randomness in bytes for the initial sharing, shared multiplication and the sacrifice required for AES S-box
Full size table

5.2 Software Implementation

CAPA is a suitable technique for software implementations if we map different tiles to different processors/cores. We do, however, need to place some constraints on the underlying hardware architecture; namely each processor should have an independent memory bank. Otherwise, a single affected tile (processor) could compromise the security of the whole system by for example dumping the entire memory contents (including all shares for sensitive variables).

This model therefore does not perfectly fit commercial off-the-shelf multi-core architectures, but we think isolated memory regions is a reasonable assumption for future micro-processors. While we do not have access to such architecture, as a proof of concept we emulate the proposed multi-processor architecture by time-sharing a 32-bit single-core ARM Cortex-M4 processor. This proof-of-concept does not provide resistance against attacks such as the memory dump example above.

Case Study: AES S-box. Even though it is possible to implement the AES S-box using \(\mathrm {GF}(2^8)\) operations in SW also, we base our bitsliced software implementation on the principles of gate-level masking and we use the depth-16 AES S-box circuit by Boyar et al. [11] in order to provide competitive throughput. Our high-level implementation processes 32 blocks simultaneously which is compatible with the word size of our processor and can naturally be reduced. As the circuit boils down to a series of XOR and AND operations over pairs of value and tag shares, we redefine these elementary operations in the same way as previous works [3, Sect. 4]. We note that this technique is independent from the concrete design, and one could apply the same principles to different ciphers.

We create a prototype implementation in C99. This is an unoptimized implementation meant for functionality and security testing. We compile with gcc-arm 4.8.4. The 32 parallel SubBytes operations are performed in 2.52 million cycles (15ms) at 168MHz with \(m=8\) MAC tags and \(d=3\) shares. The implementation holds 41 intermediate variables in the stack (but this can be optimized); each takes \(d\cdot w\) bytes for value shares and \(m\cdot d \cdot w\) bytes for tag shares (\(w=4\) is number of bytes per word).

Experimental Validation of DPA Security. We use an STM32F407 32-bit ARM Cortex-M4 processor running the C99 implementation. We take EM measurements with an electromagnetic probe on top of a decoupling capacitor. This platform is very low noise: a DPA attack on the unprotected byte-oriented AES implementation succeeds with only 15 traces. Each trace is slightly above \(500\ 000\) time samples long and covers the entire execution of SubBytes. An exemplary trace is depicted at the top of Fig. 5.

Following the same procedure as in Sect. 5.1, we first perform a non-specific leakage detection test with the masking PRNG turned off. The results of the first-, second- and third-order leakage tests are shown on the left side of Fig. 5. Severe leakage is detected, which confirms that the setup is sound. When we plug in the PRNG, no leakage is detected with up to \(200\ 000\) traces (the statistic does not surpass the threshold \(C=\pm 4.5\)). This serves to confirm that the implementation effectively masks all intermediates, and that first- nor second-order DPA is not possible on this implementation. SPA features within an electromagnetic trace are better visible in the cross-correlation matrix shown in Fig. 6.

Fig. 5.
figure 5

Non-specific leakage detection on second-order SubBytes. Left column: masks off. Right column: masks on (200K traces). Rows (top to bottom): one exemplary EM trace, first-order t-test; second-order t-test; third-order t-test

Full size image
Fig. 6.
figure 6

Cross-correlation for second-order SubBytes. One can identify the 34 AND gates in the SubBytes circuit of Boyar et al. [11].

Full size image

Experimental Validation of DFA Security. For the purposes of validating our theoretical security claims on CAPA’s protection against fault attacks, we scale down our software AES SubBytes implementation, reducing the MAC key size to \(m=2\) and scaling down words to bits (\(k=1\)). Note that this parameter choice lowers the detection probability; the point of using these toy parameters is only to verify more comfortably that the detection probability works as expected. It is easier to verify that the detection probability is \(1-2^{-2}\) rather than \(1-2^{-40}\). This concrete parameter choice is naturally not to be used in a practical deployment.

When barring the all zeroes key, we expect the attacker to succeed with probability at most \(\frac{1}{2^{mk}-1}=\frac{1}{2^2-1}=33\%\). The instrumented implementation conditionally inserts faults in value and/or tag shares. We repeat the SubBytes execution 1000 times, each iteration with a fresh MAC key. Faults are inserted in a random location during the execution of the S-box.

We verify that single faults on only values or only tags are detected unconditionally when we bar the all-0s key. When a single-bit offset (fault) is inserted in a single tile in both the value and tag share, it is indeed detected in approximately \(66\%\) of the iterations. Inserting a single-bit offset in value share and a random-bit offset in tag share is a worse attack strategy and is detected in around \(83\%\) of the experiments. The same results hold when faults are inserted in up to \(d-1\) tiles. When the value and tag shares in all d tiles are modified and fixed to a known value, the fault escapes detection with probability one, as expected.

6 Conclusion

In this paper, we introduced the first adversary model that jointly considers side-channels and faults in a unified and formal way. The tile-probe-and-fault security model extends the more traditional wire-probe model and accounts for a more realistic and comprehensive adversarial behavior. Within this model, we developed the methodology CAPA: a new combined countermeasure against physical attacks. CAPA provides security against higher-order DPA, multiple-shot DFA and combined attacks. CAPA scales to arbitrary security orders and borrows concepts from SPDZ, an MPC protocol. We showed the feasibility of implementing CAPA in embedded hardware and software by providing prototype implementations of established block ciphers. We hope CAPA provides an interesting addition to the embedded designer’s toolbox, and stimulates further research on combined countermeasures grounded on more formal principles.